約数の総和

↑を読んでもよくわからないですよね。とにかく具体例を見ましょう。

例１
\(12\) の約数の総和は、\(12=2^2×3\) なので、

\((2^2+2^1+1)(3^1+1)=28\)

\(1+2+3+4+6+12=28\) で確かに求まっています。

例２
\(360=2^3×3^2×5\) の約数の総和は、

\((2^3+2^2+2^1+1)(3^2+3^1+1)(5^1+1)\)\(=1170\)

\(1+2+3+4+5+6+8+9+10+12\)\(+15+18+20+24+30+36+40+45\)\(+60+72+90+120+180+360=1170\)
で確かに求まっています。

なぜ？約数の総和の公式

素因数が \(2\) 種類のとき

\(12=2^2×3\) の約数 \(6\) 個（\(1,2,3,4,6,12\)）は以下の表にまとめられます。

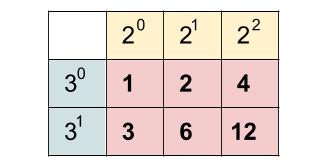
この \(6\) 個の数の和ですが、まず上の段（\(3^0\) の段）を足すと
\(1+2+4=2^0+2^1+2^2\)

下の段（\(3^1\) の段）の和は上の段の和の \(3^1\) 倍になっています。式で表すと、
\(3+6+12\)\(=2^0×3^1+2^1×3^1+2^2×3^1\)
\(=3^1(2^0+2^1+2^2)\)

よって、その和は、
\((2^0+2^1+2^2)+3^1(2^0+2^1+2^2)\)
\(=(1+3^1)(2^0+2^1+2^2)\)

もちろん \(2^0=1\) ですから、
これで約数の総和の公式通りです。

素因数が \(3\) 種類のとき

\(60=2^2×3×5\) の約数 \(12\) 個は、さきほどの表のようにはまとめられません。
\(5^0\) の表と、\(5^1\) の表の \(2\) 枚が必要です。

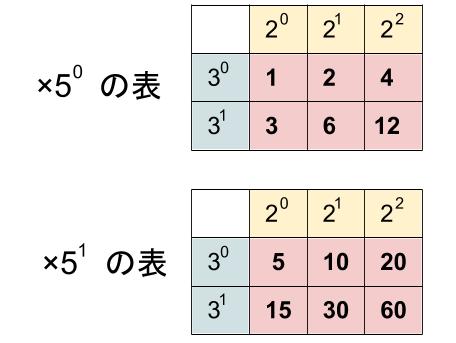
\(×5^0\) の表にある約数の和は、\(12\) の約数の和と同一で、

\((2^0+2^1+2^2)+3^1(2^0+2^1+2^2)\)
\(=(1+3^1)(1+2^1+2^2)\)

\(×5^1\) の表にある約数の和は、\(×5^0\) の表の約数の和の \(5^1\) 倍なので、

\((1+3^1)(1+2^1+2^2)×5^1\)

よって、その和は、
\((1+3^1)(1+2^1+2^2)\)\(+5^1(1+3^1)(1+2^1+2^2)\)
\(=(1+5^1)(1+3^1)(2^0+2^1+2^2)\)

これで約数の総和の公式通りです。

素因数が \(4\) 種類以上のときを証明したわけではありませんが、以下同様に約数の総和の公式が使えることは納得していただけると思います。

例題１

\(1500\) の約数の総和を求めなさい。またその中で、偶数であるものの和はいくつですか。

解説

\(1500=2^2×3×5^3\)

より、\(1500\) の約数の総和は、
\((2^2+2^1+1)(3^1+1)(5^3+5^2+5^1+1)\)\(=4368\)

また偶数の約数の総和は、

\((2^2+2^1)(3^1+1)(5^3+5^2+5^1+1)=3744\)

以上求まりました。

偶数の約数の総和・くわしく解説

偶数の約数の総和が、なぜ上のように求まるのか。よくわからない人はこちらを読みましょう。

素因数が、\(3\) と \(5\) だけからなる約数の総和は、
\((3^1+1)(5^3+5^2+5^1+1)\)
ですね。
※これがわからない人は、このページをはじめから読み直すこと！

そして、\(2^1\) を素因数として持つ約数の和は、
\(2^1(3^1+1)(5^3+5^2+5^1+1)\)

そして、\(2^2\) を素因数として持つ約数の和は、
\(2^2(3^1+1)(5^3+5^2+5^1+1)\)

この合計が求める値なので、
\(2^2(3^1+1)(5^3+5^2+5^1+1)\)\(+2^1(3^1+1)(5^3+5^2+5^1+1)\)
\(=(2^2+2^1)(3^1+1)(5^3+5^2+5^1+1)\)\(=3744\)

これが答えです。

もちろん奇数の約数の和は、\(2\) を素因数として持たないので、
\(2^0(3^1+1)(5^3+5^2+5^1+1)=624\)

奇数の約数の和 \(624\)
偶数の約数の和 \(3744\)
\(2\) つ合わせて約数の総和 \(4368\) も成り立っています。