定積分と面積
定積分と面積
定積分というわけのわからない計算を練習してきました。
ようやく定積分の実用を学習します。
定積分によって、曲線と \(x\) 軸とで囲まれた部分の面積が求まるのです。
曲線が \(x\) 軸より上方にある場合
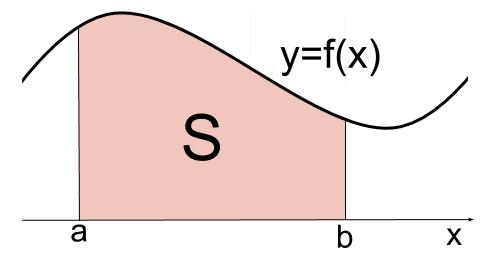
\(a \leqq x \leqq b\) において、
曲線 \(y=f(x)\) と、\(x\) 軸および \(2\) 直線 \(x=a,x=b\) とで囲まれた部分の面積 \(S\) は、
\(S=\displaystyle \int_a^b f(x) dx\)
曲線が \(x\) 軸より下方にある場合
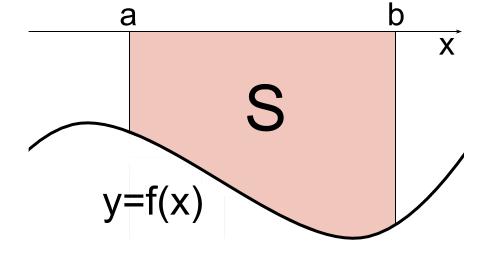
\(a \leqq x \leqq b\) において、
曲線 \(y=f(x)\) と、\(x\) 軸および \(2\) 直線 \(x=a,x=b\) とで囲まれた部分の面積 \(S\) は、
\(S=-\displaystyle \int_a^b f(x) dx\)
定積分をすることで、なんとビックリ、面積が求まるのです・・・
なんだこれ?って感じですね。
なぜ定積分で面積が求まるのか。
気になるところですが、とにかくまずは計算に習熟しましょう。
なぜ?については、別ページにて解説します。
例題1
次の曲線と直線とで囲まれた部分の面積を求めなさい。
\(y=x^2-2x+3\)
\(x=-1\)
\(x=2\)
\(x\) 軸
解説
\(y=x^2-2x+3\) のグラフが、\(-1 \leqq x \leqq 2\) で \(x\) 軸より上にあるか、下にあるかが重要です。
それを知るために、\(y=x^2-2x+3\) のグラフの概形を調べます。
右辺を平方完成して、
\(y=(x-1)^2+2\)
よって下図のようになっています。
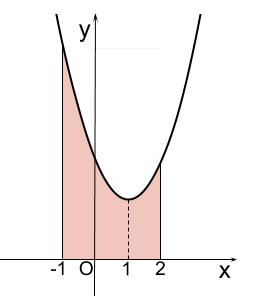
求める面積を \(S\) とすると、
\(S=\displaystyle \int_{-1}^2 (x^2-2x+3) dx\)
\(= \left[ \displaystyle \frac{1}{3}x^3-x^2+3x \right]_{-1}^2\)
\(\begin{eqnarray}= & & \displaystyle \frac{1}{3}\{2^3-(-1)^3\} \\ &-& \hspace{ 2pt }\hspace{ 7pt }\{2^2-(-1)^2\} \\ &+& \hspace{ 4pt }3\{2\hspace{ 4pt }-(-1)\hspace{ 4pt }\} \end{eqnarray}\)
\(=9\)
おススメしませんが、\(F(2)-F(-1)\) を律儀に計算するならば、
\(=\{\displaystyle \frac{1}{3}\cdot2^3-2^2+3\cdot2\}\)\(-\{\displaystyle \frac{1}{3}\cdot(-1)^3-(-1)^2+3\cdot(-1)\}\)
\(=\displaystyle \frac{14}{3}-(-\displaystyle \frac{13}{3})=9\)
例題2
次の曲線と直線とで囲まれた部分の面積を求めなさい。
\(y=x^2-x-6\)
\(x=1\)
\(x=2\)
\(x\) 軸
解説
\(y=x^2-x-6\) を平方完成すると、
\(y=(x-\displaystyle \frac{1}{2})^2-\displaystyle \frac{25}{4}\)
また、\(y=x^2-x-6=(x+2)(x-3)\)
より、グラフは下図のようになっています。
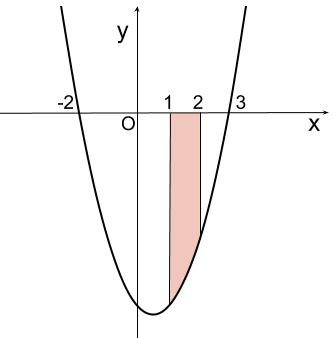
\(x\) 軸より下にあるので、マイナスをつけます。
求める面積を \(S\) とすると、
\(S=-\displaystyle \int_1^2 (x^2-x-6) dx\)
\(S=\displaystyle \int_1^2 (-x^2+x+6) dx\)
\(= \left[ -\displaystyle \frac{1}{3}x^3+\displaystyle \frac{1}{2}x^2+6x \right]_1^2\)
\(\begin{eqnarray}= &-& \displaystyle \frac{1}{3}(2^3-1^3) \\ &+& \hspace{ 1pt }\hspace{ 0pt }\displaystyle \frac{1}{2}(2^2-1^2) \\ &+& \hspace{ 3pt }6\hspace{ 2pt } (2\hspace{ 4pt }-1\hspace{ 4pt }) \end{eqnarray}\)
\(=\displaystyle \frac{31}{6}\)
例題3
次の曲線と直線とで囲まれた部分の面積を求めなさい。
\(y=-x^2+1\)
\(x=2\)
\(x\) 軸
\(y\) 軸
解説
\(-x^2+1=-(x+1)(x-1)\) なので、
\(y=-x^2+1\) のグラフは下図のようになっています。
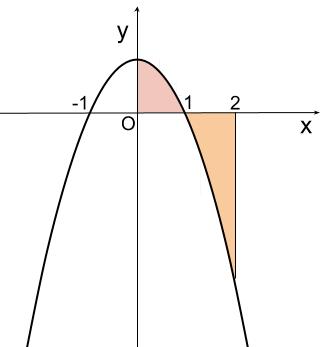
\(0 \leqq x \leqq 1\) と \(1 \leqq x \leqq 2\) で積分区間を分けます。
求める面積を \(S\) とすると、
\(S=\displaystyle \int_0^1 (-x^2+1) dx+\{-\int_1^2 (-x^2+1) dx\}\)
\(S=\displaystyle \int_0^1 (-x^2+1) dx+\int_1^2 (x^2-1) dx\)
\(= \left[ -\displaystyle \frac{1}{3}x^3+ x \right]_0^1+\left[ \displaystyle \frac{1}{3}x^3- x \right]_1^2\)
\(=\{-\displaystyle \frac{1}{3}\cdot1^3+ 1\}+\{(\displaystyle \frac{1}{3}\cdot2^3-2)-(\displaystyle \frac{1}{3}\cdot1^3-1)\} \)
\(=2\)