対数を含む関数の最大・最小

関数の最大値・最小値は必ずグラフをかいて解きます。

$2$ 次関数に帰着させる問題が定番です。

対数を扱うさい、真数条件のチェックからはじめましょう。

例題１

次の関数の最小値を求めなさい。

$y=(\log_{ 2 } x )^2-5 \cdot \log_{ 2 } x^2+10$

解説

真数条件より $x \gt 0$ かつ、$x^2 \gt 0$
つまり、$x \gt 0$ ・・・①
$\log_{ 2 } x =t$ とおくと（ $t$ の範囲は実数全体）
$\log_{ 2 } x^2=2\log_{ 2 } x=2t$

よって与えられた関数は
$y=t^2-10t+10$

平方完成して、
$y=(t-5)^2-15$

グラフは以下のようになる。

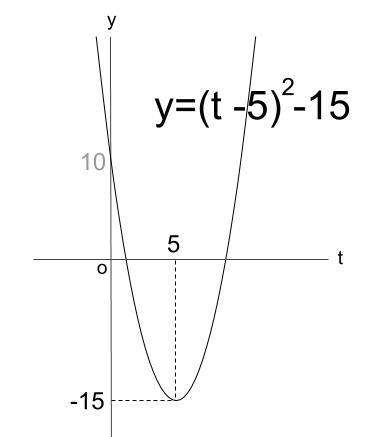
よって、$t=5$ で最小値 $-15$ をとる。

$t=5$ のとき、$\log_{ 2 } x =5$

つまり、$x=32$
これは①を満たす。

よって、$x=32$ のとき、最小値 $-15$ をとる。

例題２

$\displaystyle \frac{1}{8} \leqq x \leqq 2$ のとき、次の関数の最大値と最小値を求めなさい。

$y=(\log_{ 2 } 8x )(\log_{ 2 } 4x)$

解説

真数条件より $x \gt 0$ という定番の書き出しは不要です。
問題で $\displaystyle \frac{1}{8} \leqq x \leqq 2$ とあるからです。

では解きましょう。

$y=(\log_{ 2 } 8x )(\log_{ 2 } 4x)$

$=(\log_{ 2 } 8+\log_{ 2 } x )(\log_{ 2 } 4+\log_{ 2 } x)$

$=(3+\log_{ 2 } x )(2+\log_{ 2 } x)$

ここで、$\log_{ 2 } x=t$ とおくと

$y=(t+3)(t+2)$
この関数の最大値・最小値を調べますが、
$t$ の範囲について考察します。

$\displaystyle \frac{1}{8} \leqq x \leqq 2$ より、

底 $2$ の対数をとると、$2 \gt 1$ なので

$\log_{ 2 } \displaystyle \frac{1}{8} \leqq \log_{ 2 } x \leqq \log_{ 2 } 2$

$\log_{ 2 } \displaystyle \frac{1}{8} \leqq t \leqq \log_{ 2 } 2$

$-3 \leqq t \leqq 1$

この範囲で、$y=(t+3)(t+2)$ のグラフは下のようになります。
$y=0$ となる $x$ がわかるので、平方完成しなくとも概形がわかります。

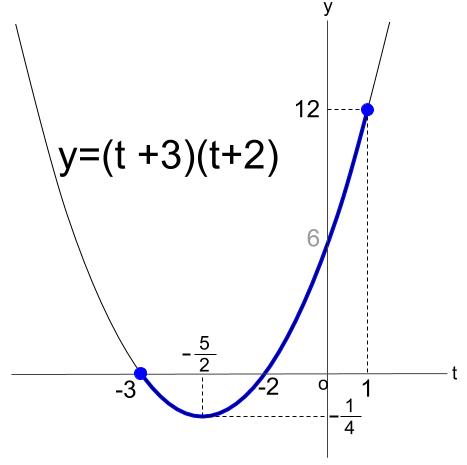
※グラフの比率は正しくありません。

頂点は $-2$ と $-3$ の中間の $-\displaystyle \frac{5}{2}$ です。
これも平方完成しなくともわかりますね。

よって、
$t=1$ 、つまり、$\log_{ 2 } x=1$ のときに最大値。
つまり、$x=2$ のときに最大値 $12$

また、
$t= -\displaystyle \frac{5}{2}$ 、つまり、$\log_{ 2 } x= -\displaystyle \frac{5}{2}$ のときに最小値。

つまり、$x=2^{-\frac{5}{2}}=\displaystyle \frac{1}{2^{\frac{5}{2}}}=\displaystyle \frac{\sqrt{2}}{8}$ のときに最小値 $-\displaystyle \frac{1}{4}$