指数関数

いよいよ指数関数について見ていきましょう。
指数関数とは \(y=a^x\) です。
\(a \gt 0\)　\(a \neq 1\) で定義されます。
\(a\) を底とする \(x\) の指数関数といいます。

指数関数のグラフ

\(y=2^x\) という関数のグラフから、
指数関数の特徴についてを見ていきましょう。

まずは結論から見てしまいましょう。
\(y=2^x\) のグラフは以下のようになります。

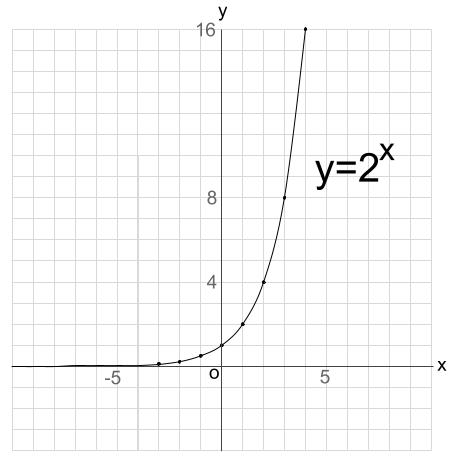
当然ですが、
\(y=2^x\)
に、さまざまな数値を入れて計算してグラフを得ます。
\(x=3\) のとき \(y=8\)
\(x=2\) のとき \(y=4\)
\(x=1\) のとき \(y=2\)
\(x=0\) のとき \(y=1\)
\(x=-1\) のとき \(y=\displaystyle \frac{1}{2}\)
\(x=-2\) のとき \(y=\displaystyle \frac{1}{4}\)
などです。
そして、
\(x=0.1\) や \(x=0.01\) など、あらゆる \(x\) で\(y\) の値が計算されます。
それらを座標として、無限個の点の集合が、\(y=2^x\) のグラフとなります。

\(x\) がほんの少し大きくなると、\(y\) は急激に大きくなります。
上図においても \(x=5\) のときの \(y=32\) は図におさまりきりません。
\(x=10\) なら \(y=1024\) です。

同様に、\(x\) がほんの少し小さくなると、\(y\) は急激に小さくなります。
上図においても \(x=-5\) のときの \(y=\displaystyle \frac{1}{32}\) あたりから
グラフと \(x\) 軸が近づきすぎて、よくわからなくなっています。

\(x\) がどれだけ小さな値になっても、\(y\) は決して \(0\) にはなりません。
グラフはいつまでも \(x\) 軸の上方にあります。
\(x\) をどこまで小さくしても、 \(y\) は限りなく小さくなりますが、常に \(y \gt 0\) です。
これを、 \(y=2^x\) のグラフは、\(x\) 軸を漸近線にもつ、といいます。

指数関数のグラフの概形

\(y\) の値が大きくなりすぎる、小さくなりすぎる。
これらの理由から、指数関数のグラフは、
大雑把な概形をとらえればＯＫで、あまり精密にかくことは必要ありません。
他の単元のグラフも同様に精密さはいらないのですが、
指数関数のグラフは特にそうです。

\(y=2^x\) のグラフも下図のようにかいておけばＯＫです。

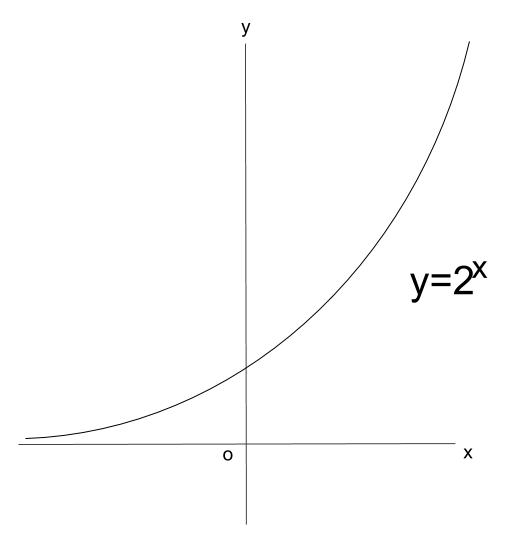
\(y=3^x\) も、\(y=1.5^x\) も、\(1 \lt a\) ならば、
大雑把な概形は上のような右上がりの単調増加のグラフになります。

指数関数 \(y=a^x\) 、\(0 \lt a \lt 1\) のグラフの概形

一方、\(0 \lt a \lt 1\) ならば、右下がりの単調減少のグラフになります。
例
\(y=(\displaystyle \frac{1}{2})^x\)

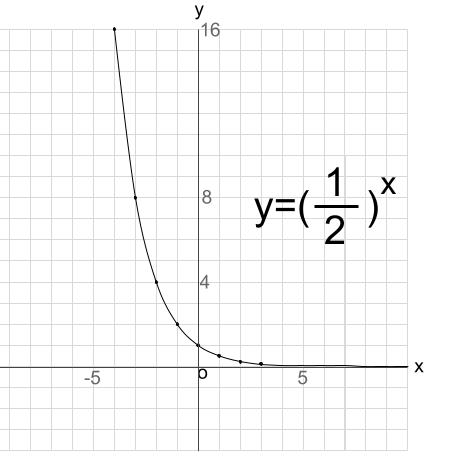
こちらのグラフも \(x\) 軸を漸近線にもちます。
\(x\) をどこまで大きくしても、 \(y\) は限りなく小さくなりますが、常に \(y \gt 0\) です。

大きくわけて指数関数のグラフは、
上の \(2\) つに分類されます。他はありません。

指数関数のグラフのまとめ

\(y=a^x\) のグラフ

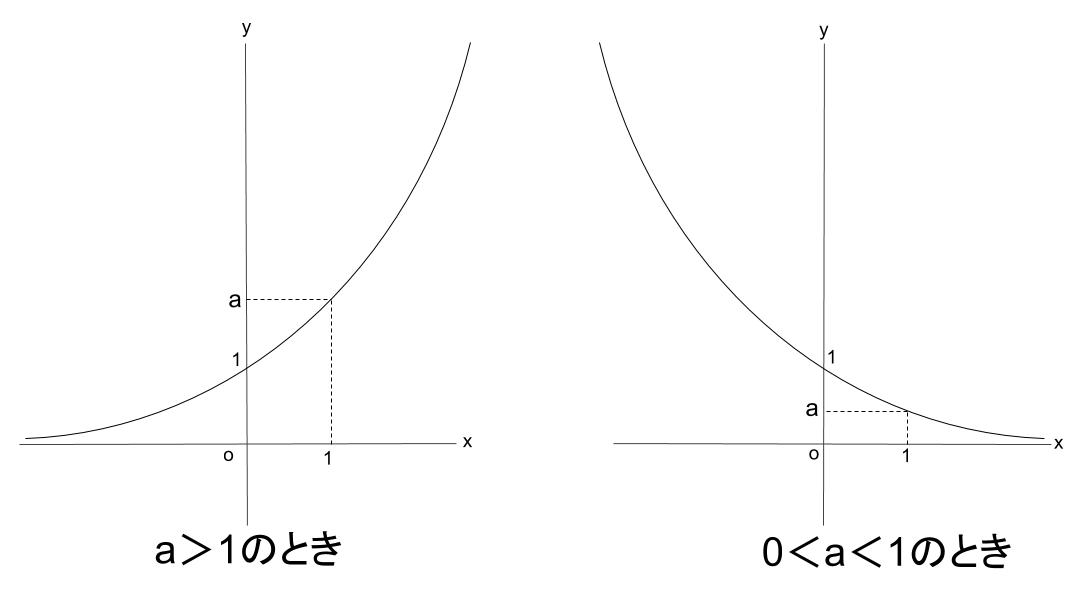
\(2\) つのグラフは \(y\) 軸で線対称となっています。

どちらの場合にも、共通する以下の \(3\) 点を必ず暗記しましょう！

定義域と値域

定義域は実数全体、値域は正の数全体
定義域　\(-\infty \lt x \lt \infty\)
値域　　\(0 \lt y \lt \infty\)
※中学数学では変域と呼んでいたものです。

必ず通る \(2\) 点

必ず、\((0,1)\) を通る。\(a^0=1\) だからです。
必ず \((1,a)\) を通る。\(a^1=a\) だからです。

\(x\) 軸を漸近線にもつ

グラフは \(x\) 軸に限りなく近づくが、決して接することも、交わることもない。
このことを、 \(x\) 軸を漸近線にもつ、といいます。

例題１

\(y=(\displaystyle \frac{1}{3})^x\) のグラフをかきなさい。

解説

まず暗記しておくべきことですが、
指数関数のグラフの概形です。
単調減少の曲線です。
※\(1 \lt a\) ならば、単調増加です。

そして \(x\) 軸は漸近線です。
\(x\) 軸に沿ってグラフは寝そべっていき、そのまま平行になるような、
そして決して交わらない。

そして、\(x=0,1\) は必ずかきましょう。

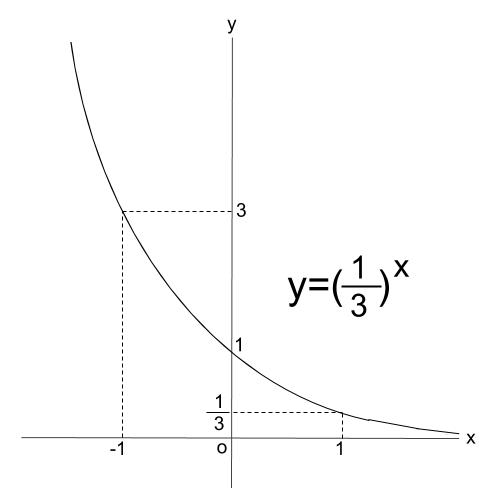
他の値は計算してられません。
なめらかに曲線でつなげばOKです。

採点対象とはならないであろう、 \(x=-1\) も意識できるとなお良いでしょう。

グラフの比率を、正確にかくことはあまり意識しないでよいです。

参考・指数が無理数のとき

数学の定義に厳密な人は、上の内容では触れられていない事項が気になっているかもしれません。

指数が無理数のときです。

大部分の高校生はこのことを無視してしまって良いと思いますが
一応軽く触れておきます。

例えば
\(2^{\sqrt{2}}\) はどのような値なのか。
ずばり
\(\sqrt{2}=1.41421356・・・\)
なので
\(2^{\sqrt{2}}=2^{1.41421356・・・}\)
を極限までつきつめた値なのです。

その値が \(1\) つに定まるといえるのか、
ということが数学的には問題となるのですが、
\(1\) つに定まります。

だから、指数関数のグラフは滑らかにつながっているのです。

大部分の高校生には興味のない話題でしょうから、これ以上深入りはしません。
興味のある人は他サイト、書籍で探求してください！