斜辺の長さが $1$ の直角三角形

サインとコサインを長さとして扱う

三角比は角度のみで定まり、直角三角形のサイズには無関係であることを
確認しました。

そこで・・・

斜辺の長さが $1$ の直角三角形で三角比を見てみましょう。

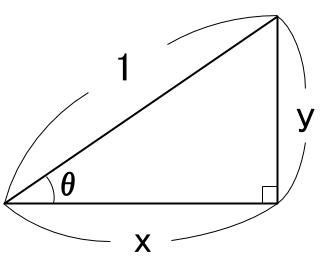
サインとコサインは以下のようになります。

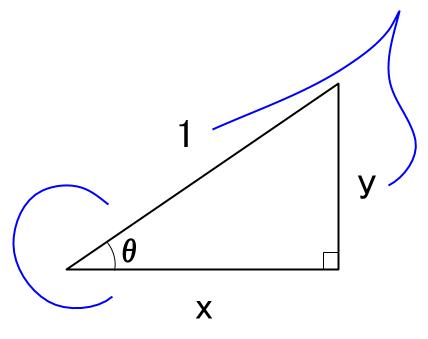
サイン
$\sin \theta=\displaystyle \frac{y}{1}=y$

コサイン
$\cos \theta=\displaystyle \frac{x}{1}=x$

つまり、$\sin \theta$ と $\cos \theta$ の値を「直角三角形の辺の長さ」として
扱うことができるようになりました。

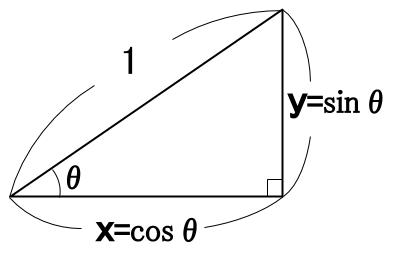
比という漠然とした値を扱うよりも、
「長さ」という具体物を扱う方がいろいろ考えやすいことも多いでしょう。

今後はこの、斜辺の長さが $1$ の直角三角形もどんどん活用していきます。

タンジェントは、直線の傾き

$\tan \theta=\displaystyle \frac{y}{x}$

タンジェントは、斜辺の長さとは無関係な値です。

タンジェントは、直線の傾きです。
中学 $2$ 年生のときに学習した $1$ 次関数の傾きです。
斜辺の傾きを表しています。

三角比の相互関係

三角比の相互関係として、代表的な $3$ つの式があります。
必ず暗記しましょう。

• $\sin^2 \theta +\cos^2 \theta =1$
• $\tan \theta=\displaystyle \frac{\sin \theta}{\cos \theta}$
• $\tan^2 \theta+1=\displaystyle \frac{1}{\cos^2 \theta}$

以下、どのように導かれるのかを見ていきましょう。

三角比の相互関係の導出

タンジェントに関して、以下の式が成り立ちます。

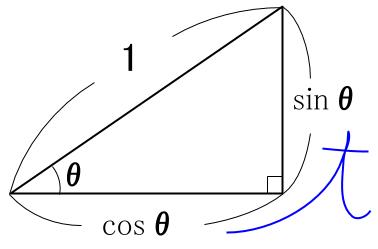
$\tan \theta=\displaystyle \frac{\sin \theta}{\cos \theta}$

これは $2$ つめの式になります。

さらに、この直角三角形に三平方の定理を適用すると、
$1$ つめの式が導かれます。

$\sin \theta × \sin \theta+\cos \theta × \cos \theta=1^2$

ちなみに、$\sin \theta × \sin \theta=\sin^2 \theta$ と表記します。
ただの決め事なので覚えるしかありません。

この表記で改めて三角比の相互関係・その１をかきます。

$\sin^2 \theta +\cos^2 \theta =1$

この式の両辺を $\cos^2 \theta$ で割ると

$\displaystyle \frac{\sin^2 \theta}{\cos^2 \theta}+\displaystyle \frac{\cos^2 \theta}{\cos^2 \theta}=\displaystyle \frac{1}{\cos^2 \theta}$

$\tan \theta=\displaystyle \frac{\sin \theta}{\cos \theta}$ なので

$\tan^2 \theta=\displaystyle \frac{\sin^2 \theta}{\cos^2 \theta}$ であり、これを使うと

$\tan^2 \theta+1=\displaystyle \frac{1}{\cos^2 \theta}$

これで $3$ つめの式が導けました。

$1$ つめと $2$ つめの式は直感的な理解をしてください。
$3$ つめは公式として覚えておきましょう。

例題１

$\sin \theta=\displaystyle \frac{1}{3}$ のとき、$\cos \theta$ と $\tan \theta$ の値を求めなさい。ただし $\theta$ は鋭角とする。

解説

先の三角比の相互関係を使えば、ただの計算問題です。

$\sin^2 \theta +\cos^2 \theta =1$
に、$\sin \theta=\displaystyle \frac{1}{3}$ を代入すれば、

$\cos^2 \theta=\displaystyle \frac{8}{9}$

$\cos \theta=\pm \sqrt{\displaystyle \frac{8}{9}}$

$\theta$ は鋭角なので、$\cos \theta$ は $0$ より大きい。

よって、

$\cos \theta= \sqrt{\displaystyle \frac{8}{9}}$

$=\displaystyle \frac{2\sqrt{2}}{3}$

また、

$\tan \theta=\displaystyle \frac{\sin \theta}{\cos \theta}$

に、$\sin \theta=\displaystyle \frac{1}{3}$ と $\cos \theta=\displaystyle \frac{2\sqrt{2}}{3}$

を代入すれば、$\tan \theta$ が求まる。

$\tan \theta=\displaystyle \frac{\sin \theta}{\cos \theta}$

とは、
$\tan \theta=\sin \theta ÷ \cos \theta$
のことなので、

$\tan \theta=\displaystyle \frac{1}{3} ÷ \displaystyle \frac{2\sqrt{2}}{3}$

$=\displaystyle \frac{1}{2\sqrt{2}}= \displaystyle \frac{\sqrt{2}}{4}$

別解１

$\sin \theta=\displaystyle \frac{1}{3}$ となる直角三角形をかいてみましょう。

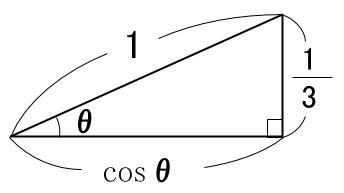
あとは三平方の定理を使えば、直角三角形の横の長さ、 $\cos \theta$ が求まります。

$\cos \theta=\displaystyle \frac{2\sqrt{2}}{3}$

$\tan \theta$ は定義どおり計算します。

別解２

もちろん、斜辺が $1$ でない直角三角形で解いても構いません。

$\sin \theta=\displaystyle \frac{1}{3}$ なのですから下図です。

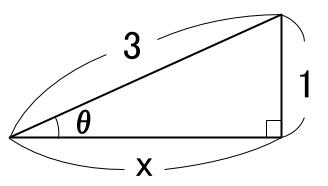
三平方の定理で $x$ を求めて、
あとは三角比の定義通りに比の値を求めます。
こちらの方が計算が楽かもしれまんせん。

例題２

$\tan \theta=3$ のとき、$\sin \theta$ と $\cos \theta$ の値を求めなさい。ただし $\theta$ は鋭角とする。

解説

相互関係からガツガツ計算して解いてもよし。
図形的に解いてもよし。

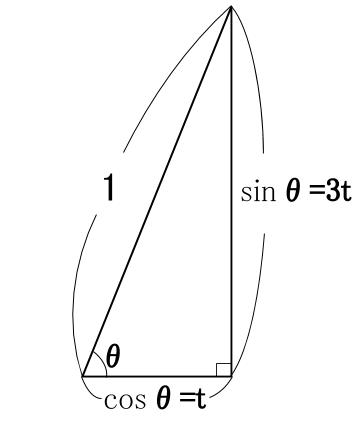
この図で解くならば、三平方の定理より
$1^2=t^2+(3t)^2$
$t$ は $0$ より大きいので

$t=\displaystyle \frac{\sqrt{10}}{10}$

よって

$\cos \theta=t=\displaystyle \frac{\sqrt{10}}{10}$

$\sin \theta=3t=\displaystyle \frac{3\sqrt{10}}{10}$