弧度法なんて怖くない

弧度法って何なのコレ・・・

唖然とする高校生を大量生産する「弧度法」

まずは徹底的な「丸暗記」をして慣れていただく、それだけです！！

\(45°=\displaystyle \frac{\pi}{4}\)

\(180°= \pi\) です。

これをとにかく暗記してください。
これさえ覚えておけば、他はすべて比例計算で求めることができます。

\(180°= \pi\) の半分は、

\(90°=\displaystyle \frac{\pi}{2}\)

計算で求められますが、直角は \(\displaystyle \frac{\pi}{2}\)
非常に良く使うので丸暗記しましょう。

さらに半分は

\(45°=\displaystyle \frac{\pi}{4}\)

これも自然と暗記してしまいますね。

\(45°\) きざみの角が弧度法でどうなるのかを図で見ておきましょう。
半円が \(\pi\) です。この半円が基準です。
半円を \(4\) 等分したもの、 \(2\) 等分したもの、
図で視覚的にも覚えてしまいましょう。

すべてを急いで丸暗記しなくとも、\(180°= \pi\) さえ覚えていれば
求められますね。

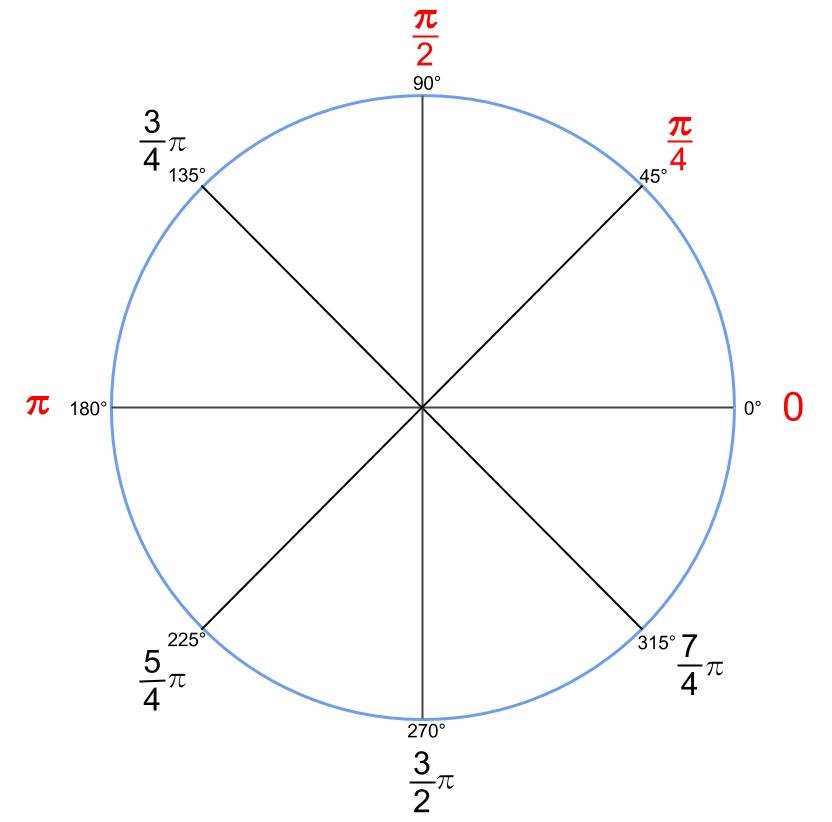
赤字のものは丸暗記してしまいましょう。

\(60°=\displaystyle \frac{\pi}{3}\)

\(180°= \pi\) なので、

これの \(\displaystyle \frac{1}{3}\) は

\(60°=\displaystyle \frac{\pi}{3}\)

これの \(2\) 倍は

\(120°=\displaystyle \frac{2\pi}{3}\)

計算ですぐに求められますが、できるだけはやく丸暗記です。

\(60°\) きざみの角が弧度法でどうなるのかの図です。
\(240°,300°\) は急いで丸暗記しなくともＯＫです。
丸暗記していなくとも、容易に求められますからね。

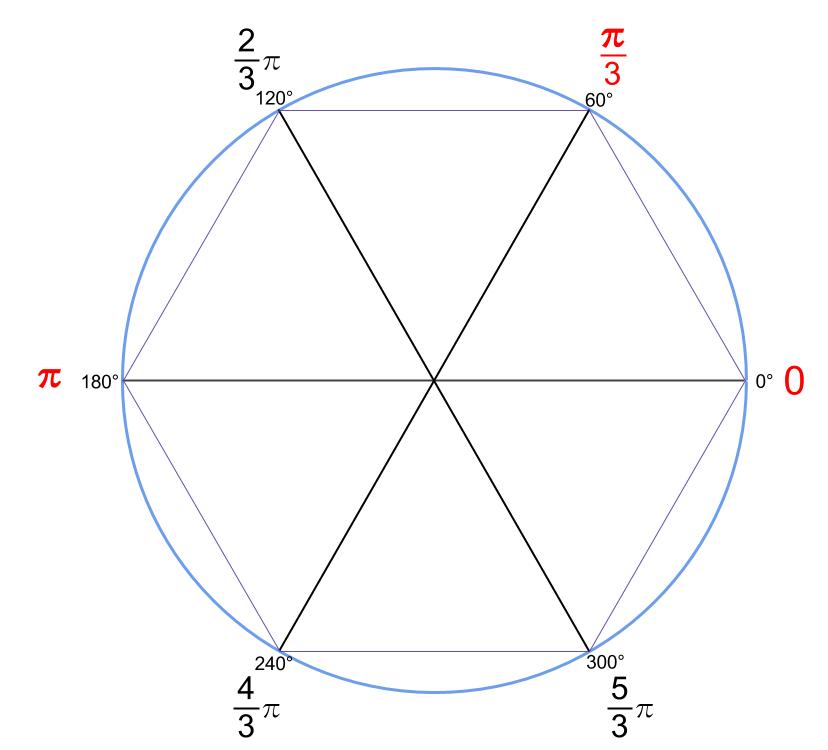
赤字のものは丸暗記してしまいましょう。

\(30°=\displaystyle \frac{\pi}{6}\)

\(60°=\displaystyle \frac{\pi}{3}\) なので、

これの半分は

\(30°=\displaystyle \frac{\pi}{6}\)

これも 計算ですぐに求められますが、できるだけはやく丸暗記しましょう。

\(30°\) きざみの角が弧度法でどうなるのかの図は、\(60°\) きざみの
細かい版です。
\(180°\) を超えた角は急いで丸暗記しなくてもＯＫです。
容易に求められますね。

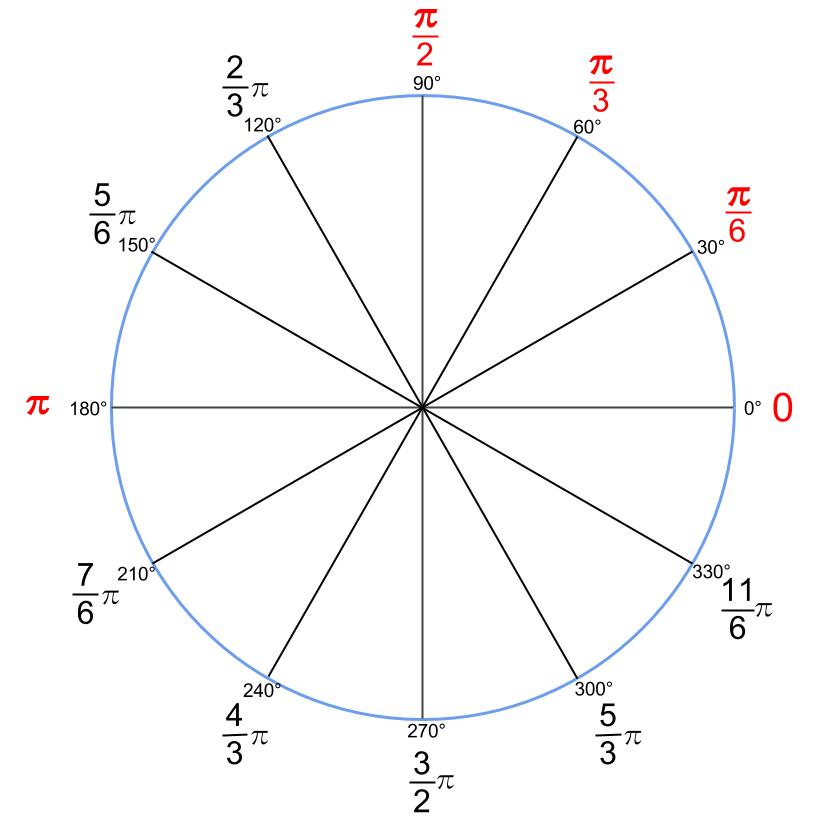
赤字のものは丸暗記してしまいましょう。

例題１

\(1\) ラジアンは度数法で何度ですか。
また度数法で \(1\) 度を、弧度法で表しなさい。

解説

大学入試ではまず見ない問題ですが、
学校の定期テストで出題されるタイプです。

\(180°= \pi\) なので、

両辺を \(\pi\) で割れば、

\(\displaystyle \frac{180°}{\pi} = 1\)

よって、 \(1\) ラジアンは \(\displaystyle \frac{180°}{\pi}\) です。

また、 \(180°= \pi\) の両辺を \(180\) で割れば、

\(1°=\displaystyle \frac{\pi}{180}\)

よって、度数法で \(1\) 度は、弧度法で \(\displaystyle \frac{\pi}{180}\) ラジアンです。

※ラジアンはつけなくて可

例題２

次の度数は弧度に、弧度は度数にそれぞれ直しなさい。

（１）\(450°\)
（２） \(-60°\)

（３） \(\displaystyle \frac{\pi}{12}\)

（４） \(-\displaystyle \frac{\pi}{5}\)

解説

\(180°= \pi\) を覚えて、あとは比例計算をするだけです。

（１）\(450°\)
\(90°=\displaystyle \frac{\pi}{2}\) の \(5\) 倍なので、

\(450°=\displaystyle \frac{5}{2}\pi\)

以下同様の比例計算です。答えのみ記しておきます。
（２） \(-60°=-\displaystyle \frac{\pi}{3}\)

（３） \(\displaystyle \frac{\pi}{12}=15°\)

（４） \(-\displaystyle \frac{\pi}{5}=-36°\)

Copyright secured by Digiprove © 2020 ko-su- info