弧度法のメリット
弧度法って結局何なの?
弧度法の導入のページでかきました。
弧度法って結局なんなの?という疑問は一回捨てよう。
とにかく慣れることが最優先、と。
その理由として
- 結局慣れて実際の計算をしていかないと、メリットはわからない
- そもそもの話も大事だけど、まずは目の前のテストで点数を取れ!
の2点でしょうか。
しかし、弧度法って結局なんなの?
という好奇心を持つことはとても大事ですので、
弧度法とは結局何なのかについて以下書いていきます。
弧度法が最も自然な定義
実は・・・
弧度法でないといけない数学的必然性はありません。
つまり、度数法のまま数学を構築、記述していくことは可能です。
しかし・・・
度数法を用いると、
さまざまな式に \(\displaystyle \frac{\pi}{180}\) という比例定数が現れます。
これがものすごく汚いんです。
しかし、弧度法を用いると汚い比例定数が消えるんです。
※一般相対性理論もそうです。理論から構築していきますが、
最後は現実に知られているニュートン力学とあわせるために比例定数を決めます。
理論から必然的に比例定数が決まるわけではないのです。
現段階では、なんのことだかわからなくて結構です。
弧度法でないといけない数学的必然性はない。
しかし、
汚い比例定数が消えるような定義である弧度法が最も自然な角の測り方である、ということです。
一回転が \(360\) である必然性はない
弧度法の導入を思い出してください。
あるいは、もう一度読み返してください。
「なんと自然な角の定義だ」って思いませんか?
あれ?思わないですかね。
でも度数法の不自然さならわかるでしょう。
度数法は明らかに不自然です。
なぜ \(360\) などという数値を持ち出したのでしょう?
非常に恣意的です。人工的です。自然さは一切ありません。
もちろん日常的感覚で言えば、
度数法に対する親しみは一生消えないレベルで沁みついているでしょう。
しかし、冷静になって考えてみれば、度数法の不自然さは明らかです。
\(1\) 回転を \(360°\) と決める必然性はまったくありません。
度数法は非常に人工的な定義です。
弧度法の最も美しい定義
多くの教科書にのっている弧度法の定義を読んで、
「なんと自然で美しい定義だ・・・」
と思えないですよね。
「定義」は、まったく同じことでも違う言い方で定義することができます。
弧度法とはどれほど自然で美しい定義なのか、それを痛感してもらいましょう。
以下に示すのが、最もおススメする弧度法の定義です。
やはり単位円に登場してもらいましょう。
半径 \(1\) の動径 \(OP\) が 始線 \(OX\) から回転する。
回転によってできたおうぎ形の弧の長さを、角の大きさとする。
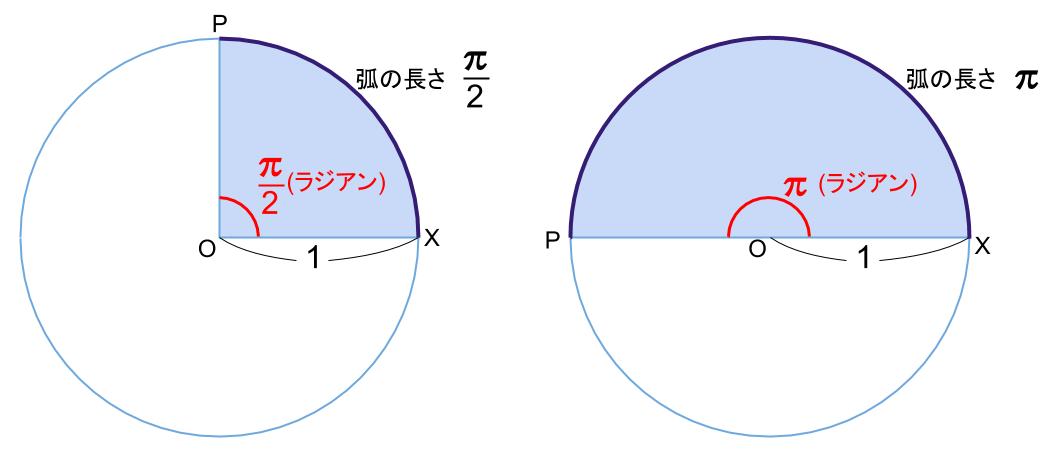
\(90°\) で \(\displaystyle \frac{\pi}{2}\)
半回転で \(\pi\)
一回転で \(2\pi\)
です。
小学校以来、角の大きさをどのように図示してきましたか?
「小さい弧」
で図示してきましたよね!?
おうぎ形の弧と、その中心角を表す曲線って同じなんですよ。
弧が角の大きさを表しているって自然じゃないですか。
※ところで、正確には、「弧の長さを、角の大きさとする」は間違いです。
これでは、角の大きさの単位が \(cm\) となってしまいます。
はじめの弧度法の導入時に説明したとおり、弧の長さ \(cm\) を半径 \(cm\) で割った無次元量が弧度法の単位であり、つまり「単位なし」です。
弧度法による美しい公式
度数法の不自然さ
弧度法の美しさ
お分かりいただけたでしょうか?
度数法の不自然さなら、なんとなくわかったような気がする・・・
という感覚をつかんだ人の中にも、
でも弧度法がベストな理由がピンとこない!
という思いが消えない人が多いことでしょう。
そうですね。
ずばり先人たちの研究成果を見ることにしましょう。
弧度法が最も自然な定義なのです。
・正弦の極限
\(\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin x}{x} =1\)
・正弦の微分と余弦の微分
\((\sin x)´=\cos x\)
\((\cos x)´=-\sin x\)
・正弦のマクローリン展開
\(\sin x=x- \displaystyle \frac{x^3}{3!}+ \displaystyle \frac{x^5}{5!} – \displaystyle \frac{x^7}{7!}+ \ldots\)
三角関数なんてまだ習っていない!という人もいるでしょう。
極限?微分?
そんなの知らない!!という人もいるでしょう。
よくわからないまま、式を眺めてもらえば結構です。
これを度数法で表示すると
・正弦の極限
\(\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin x}{x} =\displaystyle \frac{\pi}{180}\)
・正弦の微分と余弦の微分
\((\sin x)´=\displaystyle \frac{\pi}{180}\cos x\)
\((\cos x)´=-\displaystyle \frac{\pi}{180}\sin x\)
・正弦のマクローリン展開
\(\sin x=\displaystyle \frac{\pi}{180}x- \displaystyle \frac{\pi^3}{180^3}\displaystyle \frac{x^3}{3!}+ \displaystyle \frac{\pi^5}{180^5}\displaystyle \frac{x^5}{5!} – \displaystyle \frac{\pi^7}{180^7}\displaystyle \frac{x^7}{7!}+ \ldots\)
一目瞭然ですね。
\(\displaystyle \frac{\pi}{180}\) が現れないような定義をしようと思うのは
自然なことでしょう。
ちなみに、
「三角関数」は弧度法の練習のすぐあとに学習します。
「微分」は、文系の人は \(f(x)=x の n 次式\) の微分まで学習します。
「三角関数の微分」は理系の人のみです。
「マクローリン展開」は大学数学です。
現段階では「なんだが不思議な美しい式だな」って感じてもらえればそれで十分です。
弧度法の恩恵は数学Ⅲから
あれ?あれ?気づきました?
つまり・・・
文系の人は
「弧度法の美しさ、弧度法の計算の必然性を体験することなく高校数学を終える」ことになります。
それなのに、弧度法の習得をしなくてはなりません・・・
アメリカに移住しないのに、フィート、インチを習得するようなものですが、
まあ入試にでるので・・・やるしかありませんね。