角の2等分と線分の比
角の2等分と線分の比
必ず暗記しないといけない下の定理があります。
下図のように、角 \(A\) の \(2\) 等分線と、\(BC\) の交点を \(D\) とします。
このとき、\(BD:DC=AB:CA\)

なぜか、「~の定理」という名前がついていません。
しかし、非常によく出題されます。
極めて覚えやすい定理ですね。しっかり暗記しましょう。
角の2等分と線分の比の証明
下図のように、\(AD\) と平行な線分 \(EC\) を引きます。
いわゆるピラミッド型相似ができます。
三角形 \(BDA\) と三角形 \(BCE\) が相似です。
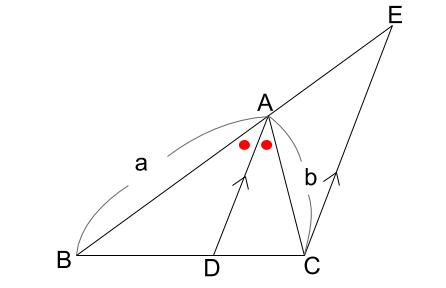
また、平行線の錯角より、\(DAC=ECA\)
また、平行線の同位角より、\(BAD=AEC\)
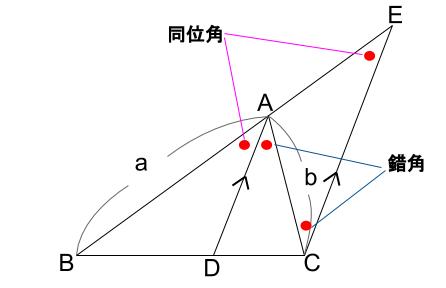
このことから、三角形 \(ACE\) は、二等辺三角形です。
したがって、\(AC=AE=b\)
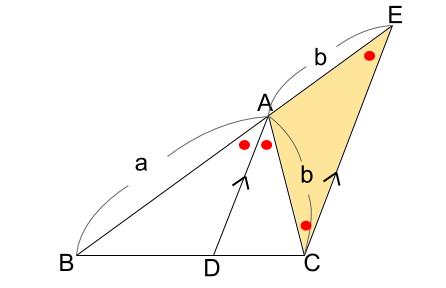
さて、ピラミッド型相似に注目しましょう。
\(BA:AE=a:b\) ですので、
\(BD:DC=a:b\) も成り立ちます。
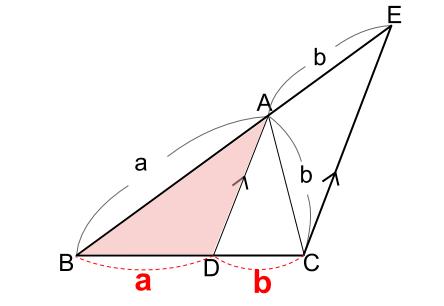
以上で証明終了です。
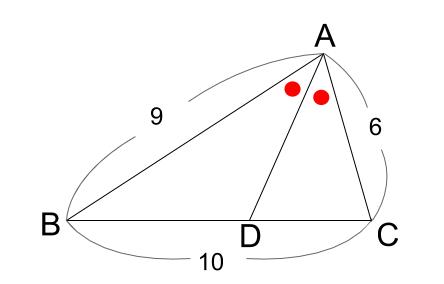
例題1
下の図において、\(AD\) は角 \(A\) の \(2\) 等分線です。
\(BD\) の長さを求めなさい。
解説
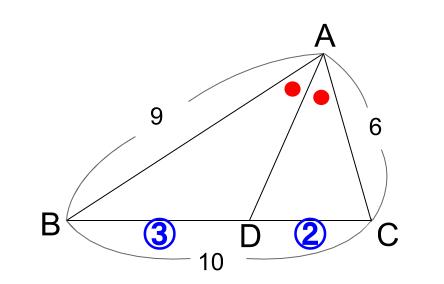
角の \(2\) 等分と線分の比の性質を使うのみです。
\(BD:DC=9:6=3:2\) なので、
\(BD=10×\displaystyle \frac{3}{3+2}=6\)
以上、求まりました。
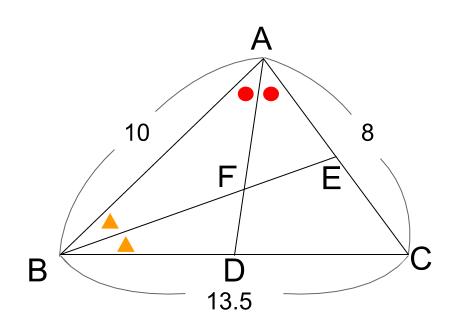
例題2
下の図において、\(AD\) は角 \(A\) の \(2\) 等分線であり、\(BE\) は角 \(B\) の \(2\) 等分線です。
\(AF:FD\) を求めなさい。
解説
角の \(2\) 等分があるので、線分の比が求められます。
角の \(2\) 等分と線分の比の性質を使いましょう。
角 \(A\) の\(2\) 等分線より、
\(BD:DC=10:8=5:4\)
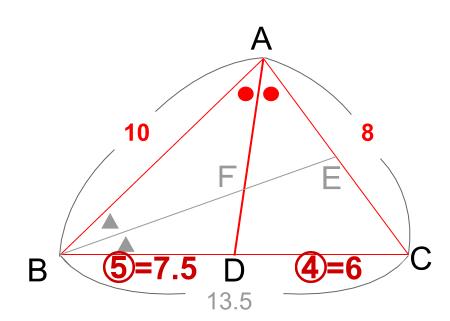
\(BD=13.5×\displaystyle \frac{5}{5+4}=7.5\)
次に、角 \(B\) の\(2\) 等分線より、
\(AF:FD=10:7.5=4:3\)
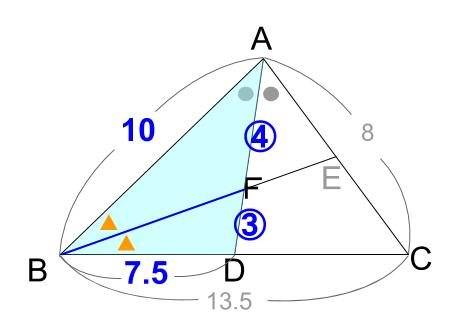
以上求まりました。