円の方程式

「標準形」は、中心と半径がわかる形です。
特に、中心が原点 \((0,0)\) のときは、
\(x^2+y^2=r^2\)
です。

「一般形」は、標準形を展開したもので、
\(x^2+y^2+lx+my+n=0\)
の形になります。
\(l,m,n\) はそれぞれ \(0\) になることもあります。
つまり、
\(x^2+y^2+4x-3y=0\)
や
\(x^2+y^2-5x+4=0\)
や
\(x^2+y^2+2y=0\)
のような円の方程式もあります。

\(x^2\) と \(y^2\) の項は、両方ないと「円」ではなくなります。
また、\(x^2\) と \(y^2\) の係数は等しくないと「円」ではありません。

なぜ？円の方程式

なぜ、\((x-a)^2+(y-b)^2=r^2\) が円を表すのでしょうか。

「まずは深く考えないで覚えてしまえ！」

と思いますが・・・

確認しておきましょう。

まず
\(x^2+y^2=r^2\)
が原点 \((0,0)\) を中心とする半径 \(r\) の円になることを確かめておきましょう。

\(x^2+y^2=r^2\) という式を満たす、無数の点 \(P(x,y)\) を座標平面上にとっていくわけです。

ところで、この式って「三平方の定理」を表していますね。
斜辺 \(PO\) の長さが \(r\) の直角三角形の頂点 \(P\) の座標が、この式
\(x^2+y^2=r^2\) を満たします。

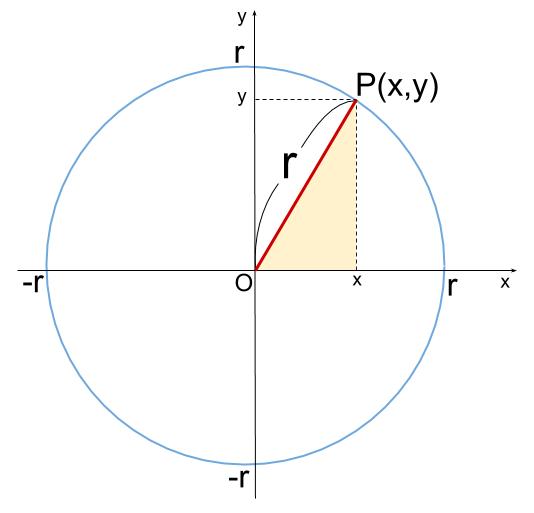
点 \(P\) は、半径 \(r\) の円をえがきますね。

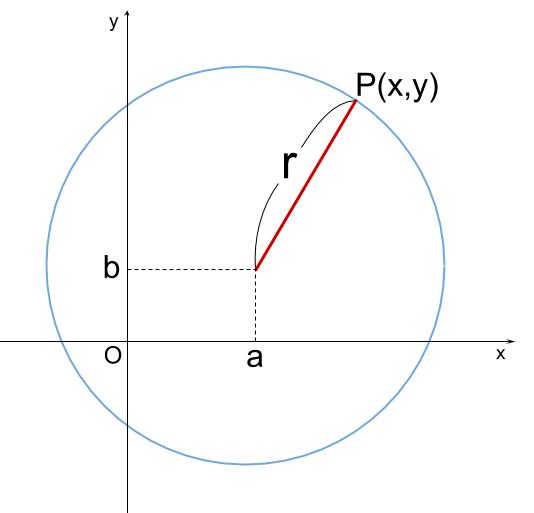
あとは、この円を平行移動すれば、座標平面上のどこにでも円をえがけます。
\(x\) 方向に \(a\)
\(y\) 方向に \(b\)
平行移動させれば、
\((x-a)^2+(y-b)^2=r^2\) となります。

先ほども書いた通りですが、なんとなく雰囲気がわかった程度で、
とにかく「円の方程式を暗記」してしまう、という学習法で構いません。
まずは、慣れてしまいましょう。
基本問題が解けるようになりましょう。
深く考えたくなったら、そのときまた戻ってきて学習すればＯＫです。

例題１

中心が \((2,-3)\)、半径が \(1\) の円の方程式を求めなさい。

解説

中心と半径がわかるときは標準形を利用します。

\((x-2)^2+\{y-(-3)\}^2=1^2\)
より
\((x-2)^2+(y+3)^2=1\)
です。

例題２

\(x^2+y^2+6x-4y-3=0\) はどのような図形を表すか答えなさい。

解説

まずこの式が、「円の一般形だ！」と
わかるようになっていないといけません。
ポイントは、\(x^2\) と \(y^2\) の項の係数が等しいことです。
※もちろん \(x,y\) 以外に別の文字がないこと、など言いだしたらきりがないですけど。

さて、どのような図形か？という問いに、
「円です！」と答えても、正解とはなりません。

中心と半径を求めろ、と暗に言っているわけです。

「円の一般形」が出てきて、どのような図形を表すか答えろ、ときたら、
中心と半径を求める、つまり、「円の標準形に直せ」
という問題なんだな、と理解してください。

では、一般形を標準形に直します。
このページの最も重要な部分です。

\(x^2+y^2+6x-4y-3=0\)

まず、\(x\) チームと \(y\) チームに分けます。並べ替えます。
\(x^2+6x+y^2-4y-3=0\)

\(x\) チームで平方完成、\(y\) チームで平方完成、
それぞれ別々に行います。

まず \(x\) チームで平方完成
\(x^2+6x\)\(+y^2-4y-3=0\)
\((x+3)^2-9\)\(+y^2-4y-3=0\)

続けて、 \(y\) チームで平方完成、
\((x+3)^2-9+\)\(y^2-4y\)\(-3=0\)
\((x+3)^2-9+\)\((y-2)^2-4\)\(-3=0\)

定数項を右辺に移項してまとめます。
\((x+3)^2+(y-2)^2=16\)

これで標準形への変形が完了です！！

右辺は「半径の \(2\) 乗」なので、
\((x+3)^2+(y-2)^2=4^2\)
とさらに変形します。

よって、
中心が \((-3,2)\)、半径が \(4\) の円
が答えになります。

例題３

\(3x^2+3y^2-6y-1=0\) はどのような図形を表すか答えなさい。

解説

\(x^2\) と \(y^2\) の項の係数が等しいので、「円の一般形」です。
よって、標準形に変形しましょう。

まず、与式を \(3\) で割ります。
\(x^2+y^2-2y-\displaystyle \frac{1}{3}=0\)

\(x\) チームは平方完成が終わっています。\(x\) の \(1\) 次の項がないからです。
\(y\) チームを平方完成します。

\(x^2+\)\(y^2-2y\)\(-\displaystyle \frac{1}{3}=0\)

\(x^2+\)\((y-1)^2-1\)\(-\displaystyle \frac{1}{3}=0\)

定数項を右辺に移項してまとめます。

\(x^2+(y-1)^2=\displaystyle \frac{4}{3}\)

半径の \(2\) 乗が \(\displaystyle \frac{4}{3}\)
なので半径は、

\(\sqrt{\displaystyle \frac{4}{3}}\)

\(=\displaystyle \frac{2}{\sqrt{3}}\)

\(=\displaystyle \frac{2\sqrt{3}}{3}\)

よって、中心が \((0,1)\) で、半径が \(\displaystyle \frac{2\sqrt{3}}{3}\)の円
これが答えです。