センター試験・過去問研究

センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう！

(1)の解説

微分係数を定義にしたがって求めよという問題です。

微分の公式 $(x^n)’ =nx^{n-1}$ を暗記だけしていた受験生を振るい落とす問題で、基本公式の根本を理解しているかどうかを試す一題です。
今後も間違いなくこの方向性の出題は続くでしょう。

では、いきます。

平均変化率とは、

グラフの $2$ 点を結んだ直線の傾きのこと！

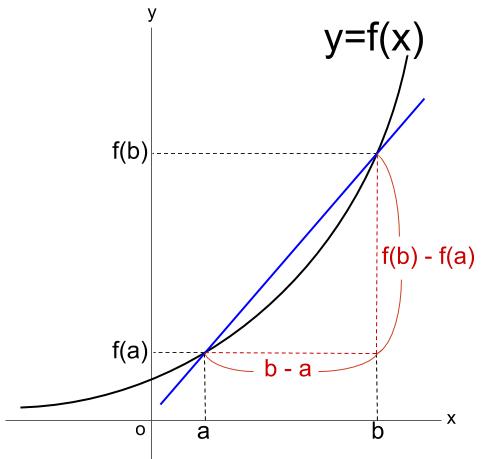
関数 $f(x)$ の $x=a$ から $x=b$ までの平均変化率は

$平均変化率 = \displaystyle \frac{yの増加量}{xの増加量} =\displaystyle \frac{f(b)-f(a)}{b-a}$

よって、 $f (x)=\displaystyle \frac{1}{2} x^2$ の $x$ が $a$ から $a+h$ まで変化するときの $f (x)$ の平均変化率は

$\displaystyle \frac{\displaystyle \frac{1}{2} (a+h)^2-\displaystyle \frac{1}{2} a^2}{(a+h)-a} =\displaystyle \frac{\displaystyle \frac{1}{2} (2ah+h^2)}{h}$

$=a+\displaystyle \frac{h}{2}$

より、ア＝a、イ＝２

そして、平均変化率の極限が「微分係数」です。

$f´(a)=\displaystyle \lim_{ h \to 0 } (a+ \displaystyle \frac{h}{2})=a$

より、ウ＝０、エ＝a

(2)の解説

$y=\displaystyle \frac{1}{2}x^2$ を $x$ で微分すると

$y´=x$

より、$P(a,\displaystyle \frac{1}{2}a^2)$ における接線の傾きは、$a$ です。

より、求める接線 $l$ の方程式は、

$y-\displaystyle \frac{1}{2}a^2=a(x-a)$

整理して

$y=ax-\displaystyle \frac{1}{2}a^2$

より、オ＝a、カ＝２

直線 $l$ と $x$ 軸との交点 $Q$ の座標は、直線 $l$ に $y=0$ を代入して、

$0=ax-\displaystyle \frac{1}{2}a^2$

$a \gt 0$ なので、$a$ で割って、

$x=\displaystyle \frac{a}{2}$

つまり、$Q(\displaystyle \frac{a}{2},0)$

より、キ＝a、ク＝２

点 $Q$ を通り $l$ に垂直な直線を $m$ とすると、

$m$ 傾きは $-\displaystyle \frac{1}{a}$ 、なので、

求める直線 $m$ の方程式は、

$y=-\displaystyle \frac{1}{a}(x-\displaystyle \frac{a}{2})$

整理して、

$y=-\displaystyle \frac{1}{a}x+\displaystyle \frac{1}{2}$

より、ケコ=－１、サ＝a、シ＝１、ス＝２

図示なしで解けますが、こんな図ですね。

ここまで、基本中の基本しか出題されていませんね！！

では後半戦です。

直線 $m$ と $y$ 軸との交点 $A$ の座標を求めましょう。

直線 $m$ の方程式は、
$y=-\displaystyle \frac{1}{a}x+\displaystyle \frac{1}{2}$ から、

$A(0,\displaystyle \frac{1}{2})$ です。

三角形 $APQ$ を図示すると、下図の赤い三角形です。
この面積 $S$ を求めます。

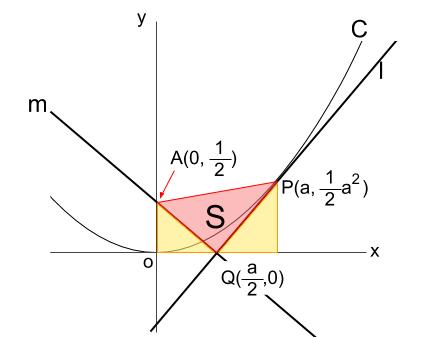
これは、「台形の面積」から「左下の三角形の面積」と「右下の三角形の面積」を引くことで求められますね。

台形の面積は、$(\displaystyle \frac{1}{2}+\displaystyle \frac{1}{2}a^2)×a×\displaystyle \frac{1}{2}=\displaystyle \frac{1}{4}a(a^2+1)$

左下の三角形の面積は、$\displaystyle \frac{1}{2}a×\displaystyle \frac{1}{2}×\displaystyle \frac{1}{2}=\displaystyle \frac{1}{8}a$

右下の三角形の面積は、 $\displaystyle \frac{1}{2}a×\displaystyle \frac{1}{2}a^2×\displaystyle \frac{1}{2}=\displaystyle \frac{1}{8}a^3$

より、$S=\displaystyle \frac{1}{4}a(a^2+1)-\displaystyle \frac{1}{8}a-\displaystyle \frac{1}{8}a^3$

$=\displaystyle \frac{a(a^2+1)}{8}$

より、セ＝１、ソ＝８

次に、$y$ 軸と線分 $AP$ および曲線 $C$ によって囲まれた図形の面積 $T$ です。

まず図示します。

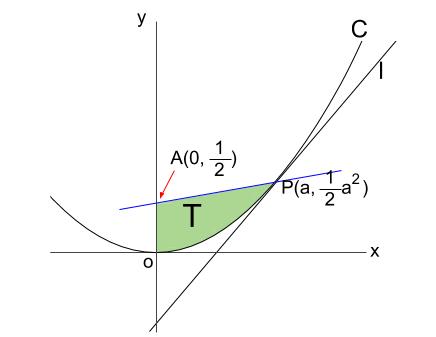
$T$ は、直線 $AP$ から 曲線 $C:y=\displaystyle \frac{1}{2}x^2$ を引いたものを積分すれば一発で求まりますね。

そのためには直線 $AP$ の方程式を求めます。

この「直線 $AP$ の方程式」を求めるのがやや面倒です。

そこで、下図のように面積 $T_{0}$ を考えます。

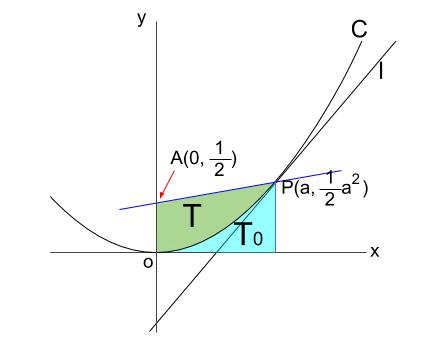
$T$ は台形の面積から、$T_{0}$ を引けば求まります。
こちらの方が計算が簡単に済みそうですね！

では行きましょう。

$T_{0}=\displaystyle \int_{0}^a \displaystyle \frac{1}{2}x^2 dx$

$= \left[ \displaystyle \frac{1}{6}x^3 \right]_{0}^a$

$=\displaystyle \frac{1}{6}a^3$

台形の面積は、先ほど三角形 $APQ$ を求めるときに求めています。

$\displaystyle \frac{1}{4}a(a^2+1)$

です。

よって、
$T=$ 台形の面積 $-T_{0}$

$=\displaystyle \frac{1}{4}a(a^2+1)-\displaystyle \frac{1}{6}a^3$

$=\displaystyle \frac{a(a^2+3)}{12}$

より、タ＝３、チツ＝１２

別解

$T$ は、直線 $AP$ から 曲線 $C:y=\displaystyle \frac{1}{2}x^2$ を引いたものを積分しても求まります。

直線 $AP$ の方程式を求めます。

$傾き=\displaystyle \frac{yの増加量}{xの増加量}$ なので、

$傾き=\displaystyle \frac{\displaystyle \frac{1}{2}a^2-\displaystyle \frac{1}{2}}{a}$

$= \displaystyle \frac{1}{2a}(a^2-1)$

切片は、$\displaystyle \frac{1}{2}$ なので、

$y=\displaystyle \frac{1}{2a}(a^2-1)x+\displaystyle \frac{1}{2}$

よって、

$T=\displaystyle \int_{0}^a \{\displaystyle \frac{1}{2a}(a^2-1)x+\displaystyle \frac{1}{2}-\displaystyle \frac{1}{2}x^2\} dx$

$= \left[ \displaystyle \frac{1}{4a}(a^2-1)x^2+\displaystyle \frac{1}{2}x-\displaystyle \frac{1}{6}x^3 \right]_{0}^a$

$=\displaystyle \frac{a}{4}(a^2-1)+\displaystyle \frac{a}{2}-\displaystyle \frac{1}{6}a^3$

$=\displaystyle \frac{a(a^2+3)}{12}$

こちらでも求まります。

では続きです。

$a \gt 0$ の範囲における $S-T$ の値について調べます。
$S-T=g(a)$ とおきます。

$g(a)=\displaystyle \frac{a(a^2+1)}{8}-\displaystyle \frac{a(a^2+3)}{12}$

$=\displaystyle \frac{a(a^2-3)}{24}$

より、テ＝３、トナ＝２４

$a \gt 0$ であるから、$S-T \gt 0$ となるような $a$ のとり得る値の範囲は $a \gt \sqrt{ニ}$ である。

$g(a)=\displaystyle \frac{a(a^2-3)}{24} \gt 0$

$\displaystyle \frac{a(a+\sqrt{3})(a-\sqrt{3})}{24} \gt 0$

より、$a \gt \sqrt{3}$

二＝３

また、$a \gt 0$ のときの $S-T$ の増減を調べると、

$g(a)$ は $a=ヌ$ で最小値 $\displaystyle \frac{ネノ}{ハヒ}$ をとることがわかる。

$g(a)=\displaystyle \frac{a(a^2-3)}{24}$

$g(a)=\displaystyle \frac{a^3-3a}{24}$

$g(a)´=\displaystyle \frac{3a^2-3}{24} =\displaystyle \frac{a^2-1}{8}=\displaystyle \frac{(a+1)(a-1)}{8}$

より、増減表は

$\begin{array}{c|ccccc} a & \cdots & -1 & \cdots & 1 & \cdots \\ \hline g’(a) & + & 0 & – & 0 & + \\ \hline g(a) & \nearrow & & \searrow & -\displaystyle \frac{1}{12} & \nearrow\end{array}$

グラフの概形

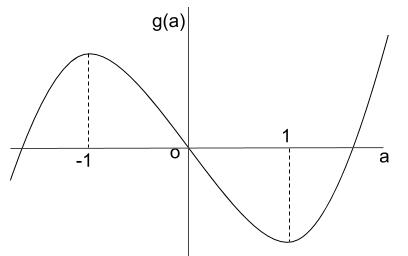
より、$a \gt 0$ のとき
$a=1$ で、最小値 $g(1)=\displaystyle \frac{1(1^2-3)}{24}=-\displaystyle \frac{1}{12}$

よりヌ＝１、ネノ＝－１、ハヒ＝１２