センター試験・過去問研究

センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう！

(1)の解説

微分係数を定義にしたがって求めよという問題です。

微分の公式 \((x^n)’ =nx^{n-1}\) を暗記だけしていた受験生を振るい落とす問題で、基本公式の根本を理解しているかどうかを試す一題です。
今後も間違いなくこの方向性の出題は続くでしょう。

では、いきます。

平均変化率とは、

グラフの \(2\) 点を結んだ直線の傾きのこと！

関数 \(f(x)\) の \(x=a\) から \(x=b\) までの平均変化率は

\(平均変化率 = \displaystyle \frac{yの増加量}{xの増加量} =\displaystyle \frac{f(b)-f(a)}{b-a}\)

よって、 \(f (x)=\displaystyle \frac{1}{2} x^2\) の \(x\) が \(a\) から \(a+h\) まで変化するときの \(f (x)\) の平均変化率は

\(\displaystyle \frac{\displaystyle \frac{1}{2} (a+h)^2-\displaystyle \frac{1}{2} a^2}{(a+h)-a} =\displaystyle \frac{\displaystyle \frac{1}{2} (2ah+h^2)}{h}\)

\(=a+\displaystyle \frac{h}{2}\)

より、ア＝a、イ＝２

そして、平均変化率の極限が「微分係数」です。

\(f´(a)=\displaystyle \lim_{ h \to 0 } (a+ \displaystyle \frac{h}{2})=a\)

より、ウ＝０、エ＝a

(2)の解説

\(y=\displaystyle \frac{1}{2}x^2\) を \(x\) で微分すると

\(y´=x\)

より、\(P(a,\displaystyle \frac{1}{2}a^2)\) における接線の傾きは、\(a\) です。

より、求める接線 \(l\) の方程式は、

\(y-\displaystyle \frac{1}{2}a^2=a(x-a)\)

整理して

\(y=ax-\displaystyle \frac{1}{2}a^2\)

より、オ＝a、カ＝２

直線 \(l\) と \(x\) 軸との交点 \(Q\) の座標は、直線 \(l\) に \(y=0\) を代入して、

\(0=ax-\displaystyle \frac{1}{2}a^2\)

\(a \gt 0\) なので、\(a\) で割って、

\(x=\displaystyle \frac{a}{2}\)

つまり、\(Q(\displaystyle \frac{a}{2},0)\)

より、キ＝a、ク＝２

点 \(Q\) を通り \(l\) に垂直な直線を \(m\) とすると、

\(m\) 傾きは \(-\displaystyle \frac{1}{a}\) 、なので、

求める直線 \(m\) の方程式は、

\(y=-\displaystyle \frac{1}{a}(x-\displaystyle \frac{a}{2})\)

整理して、

\(y=-\displaystyle \frac{1}{a}x+\displaystyle \frac{1}{2}\)

より、ケコ=－１、サ＝a、シ＝１、ス＝２

図示なしで解けますが、こんな図ですね。

ここまで、基本中の基本しか出題されていませんね！！

では後半戦です。

直線 \(m\) と \(y\) 軸との交点 \(A\) の座標を求めましょう。

直線 \(m\) の方程式は、
\(y=-\displaystyle \frac{1}{a}x+\displaystyle \frac{1}{2}\) から、

\(A(0,\displaystyle \frac{1}{2})\) です。

三角形 \(APQ\) を図示すると、下図の赤い三角形です。
この面積 \(S\) を求めます。

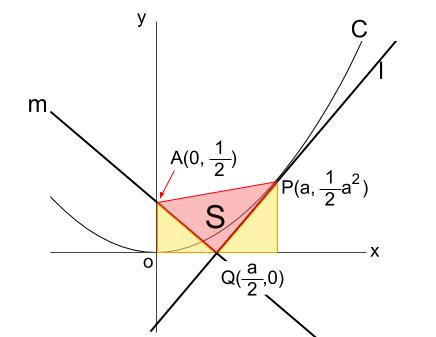
これは、「台形の面積」から「左下の三角形の面積」と「右下の三角形の面積」を引くことで求められますね。

台形の面積は、\( (\displaystyle \frac{1}{2}+\displaystyle \frac{1}{2}a^2)×a×\displaystyle \frac{1}{2}=\displaystyle \frac{1}{4}a(a^2+1)\)

左下の三角形の面積は、\(\displaystyle \frac{1}{2}a×\displaystyle \frac{1}{2}×\displaystyle \frac{1}{2}=\displaystyle \frac{1}{8}a\)

右下の三角形の面積は、 \(\displaystyle \frac{1}{2}a×\displaystyle \frac{1}{2}a^2×\displaystyle \frac{1}{2}=\displaystyle \frac{1}{8}a^3\)

より、\(S=\displaystyle \frac{1}{4}a(a^2+1)-\displaystyle \frac{1}{8}a-\displaystyle \frac{1}{8}a^3\)

\(=\displaystyle \frac{a(a^2+1)}{8}\)

より、セ＝１、ソ＝８

次に、\(y\) 軸と線分 \(AP\) および曲線 \(C\) によって囲まれた図形の面積 \(T\) です。

まず図示します。

\(T\) は、直線 \(AP\) から 曲線 \(C:y=\displaystyle \frac{1}{2}x^2\) を引いたものを積分すれば一発で求まりますね。

そのためには直線 \(AP\) の方程式を求めます。

この「直線 \(AP\) の方程式」を求めるのがやや面倒です。

そこで、下図のように面積 \(T_{0}\) を考えます。

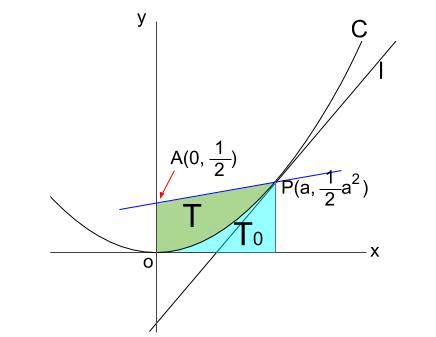
\(T\) は台形の面積から、\(T_{0}\) を引けば求まります。
こちらの方が計算が簡単に済みそうですね！

では行きましょう。

\(T_{0}=\displaystyle \int_{0}^a \displaystyle \frac{1}{2}x^2 dx \)

\(= \left[ \displaystyle \frac{1}{6}x^3 \right]_{0}^a\)

\(=\displaystyle \frac{1}{6}a^3\)

台形の面積は、先ほど三角形 \(APQ\) を求めるときに求めています。

\(\displaystyle \frac{1}{4}a(a^2+1)\)

です。

よって、
\(T=\) 台形の面積 \(-T_{0}\)

\(=\displaystyle \frac{1}{4}a(a^2+1)-\displaystyle \frac{1}{6}a^3\)

\(=\displaystyle \frac{a(a^2+3)}{12}\)

より、タ＝３、チツ＝１２

別解

\(T\) は、直線 \(AP\) から 曲線 \(C:y=\displaystyle \frac{1}{2}x^2\) を引いたものを積分しても求まります。

直線 \(AP\) の方程式を求めます。

\(傾き=\displaystyle \frac{yの増加量}{xの増加量}\) なので、

\(傾き=\displaystyle \frac{\displaystyle \frac{1}{2}a^2-\displaystyle \frac{1}{2}}{a}\)

\(= \displaystyle \frac{1}{2a}(a^2-1)\)

切片は、\(\displaystyle \frac{1}{2}\) なので、

\(y=\displaystyle \frac{1}{2a}(a^2-1)x+\displaystyle \frac{1}{2}\)

よって、

\(T=\displaystyle \int_{0}^a \{\displaystyle \frac{1}{2a}(a^2-1)x+\displaystyle \frac{1}{2}-\displaystyle \frac{1}{2}x^2\} dx \)

\(= \left[ \displaystyle \frac{1}{4a}(a^2-1)x^2+\displaystyle \frac{1}{2}x-\displaystyle \frac{1}{6}x^3 \right]_{0}^a\)

\(=\displaystyle \frac{a}{4}(a^2-1)+\displaystyle \frac{a}{2}-\displaystyle \frac{1}{6}a^3\)

\(=\displaystyle \frac{a(a^2+3)}{12}\)

こちらでも求まります。

では続きです。

\(a \gt 0\) の範囲における \(S-T\) の値について調べます。
\(S-T=g(a)\) とおきます。

\(g(a)=\displaystyle \frac{a(a^2+1)}{8}-\displaystyle \frac{a(a^2+3)}{12}\)

\(=\displaystyle \frac{a(a^2-3)}{24}\)

より、テ＝３、トナ＝２４

\(a \gt 0\) であるから、\(S-T \gt 0\) となるような \(a\) のとり得る値の範囲は \(a \gt \sqrt{ニ}\) である。

\(g(a)=\displaystyle \frac{a(a^2-3)}{24} \gt 0\)

\(\displaystyle \frac{a(a+\sqrt{3})(a-\sqrt{3})}{24} \gt 0\)

より、\(a \gt \sqrt{3}\)

二＝３

また、\(a \gt 0\) のときの \(S-T \) の増減を調べると、

\(g(a) \) は \(a=ヌ\) で最小値 \(\displaystyle \frac{ネノ}{ハヒ}\) をとることがわかる。

\(g(a)=\displaystyle \frac{a(a^2-3)}{24} \)

\(g(a)=\displaystyle \frac{a^3-3a}{24} \)

\(g(a)´=\displaystyle \frac{3a^2-3}{24} =\displaystyle \frac{a^2-1}{8}=\displaystyle \frac{(a+1)(a-1)}{8}\)

より、増減表は

\(\begin{array}{c|ccccc}
a & \cdots & -1 & \cdots & 1 & \cdots \\
\hline
g’(a) & + & 0 & – & 0 & + \\
\hline
g(a) & \nearrow & & \searrow & -\displaystyle \frac{1}{12} & \nearrow\end{array}\)

グラフの概形

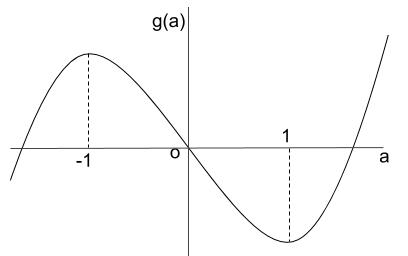
より、\(a \gt 0\) のとき
\(a=1\) で、最小値 \(g(1)=\displaystyle \frac{1(1^2-3)}{24}=-\displaystyle \frac{1}{12} \)

よりヌ＝１、ネノ＝－１、ハヒ＝１２