微分積分学の基本定理について雰囲気をつかむ

$\displaystyle \int_a^x f(t) dt$ を微分すると、もとの $f(x)$ にもどる。

「微分」と「積分」は互いに逆の演算である！画期的！！

これが「微分積分学の基本定理」の超大雑把な要約です。

現代の日本の高校生には微分積分学の基本定理は理解不能？

$\displaystyle \int_a^x f(t) dt$ は微分の逆の操作であり、これを「積分」とする。

このように積分を定義して、積分の学習をスタートする現代の日本の高校生にとって、「微分積分学の基本定理」の何が画期的なのか、わからなくて当然です。

何が画期的なのかを理解するためには、$\displaystyle \int_a^x f(t) dt$ は「微分」とまったく無関係にうまれたことを知る必要があります。

歴史的には、「積分」と「微分」はまったく無関係にうまれた別の分野なのです。

現代の数学の言葉で言うと、$\displaystyle \int_a^x f(t) dt$ は、微分とは関係のない「リーマン和の極限」というもので定義されるのです。

まったく無関係と思われていた $2$ つが結びつく！これこそが「微分積分学の基本定理」であり、人類の偉大なる大発見なのです。

$\displaystyle \int_a^x f(t) dt$ は微分の逆の操作であり、これを「積分」とするという定義から学習すると、人類の歴史的大発見の感動を追体験することができません。

以下、人類数千年の数学の発展の積み重ねを、わずか $6000$ 文字程度で追体験していきましょう！

微分積分学の基本定理は知らなくてもいい？

ちなみに・・・

大学以降も数学学習を深めていく一部の人以外は、「微分積分学の基本定理」について深く知る必要はありません。

しかし、幸か不幸か「微分積分学の基本定理」について耳にし、

言った人（先生か先輩でしょうか？）も

「微分積分学の基本定理は大事なんだよね、本当はこれを知らないとダメなんだ」
みたいなことを口にしたり・・・

こんなことを聞いてしまったら、気になりますよね。好奇心がウズウズしますね！

ということで、このページで「微分積分学の基本定理」について雰囲気をつかんでもらえたら幸いです。

しかし・・・

「微分積分学の基本定理はそもそも何なのか、という話は受験には必要ない」
ということは心に留めておいてください。

好奇心で学習を進め、深めていくことには大賛成ですが、よくわからなかったらスルーしても大丈夫です。
とりあえず目先の受験テクニックを身につけることの重大さを否定できません。
気になる人は、大学生になってから再び学習してください。

また、「微分積分学の基本定理は受験には必要ない」とは書きましたが、
どこかの難関大学が、「微分積分学の基本定理」を背景にした問題を出題することはありえます。絶対に出ないとか、まったく関係ないという意味ではないことを注意しておきます。

１．積分

積分の基本的な機能である、面積や体積の計算の芽は、数千年前の文献にも見られるそうです。
「積分」の根幹となるアイデアは、非常に微小な図形に分割して、それを集めることで面積を求めるというものです。

古代ギリシャのアルキメデス（紀元前287年から紀元前212年）が、放物線と直線に囲まれた部分の面積を求めていることが有名です。
それについてくわしく扱いませんが、図形を小さな三角形に分割し、その和の極限を求めることで面積を求めています。
これこそが「積分」の考え方であり、決して「微分の逆」などということではじまったのではありません。

さて、「積分」という言葉を使ってきましたが、アルキメデスの求積は微分の逆操作ではありません。
「積分」という言葉を使うと、「微分の逆操作」という固定概念から抜けられないですから、「積分」という言葉を使うのはちょっとやめておきましょう
アルキメデスもその後の人たちも、この操作に「積分」という名前は使っていませんでしたしね。
非常に微小な図形に分割して、それを集めることで面積を求める考え方を以降、「微集積法」と呼びましょう。
このコラム独自の言葉です。世間に広まっている言葉ではありませんよ。

この「微集積法」は、多くの学者によって使用、研究され続けました。

ドイツの天文学者ヨハネス・ケプラー（1571年から1630年）は、惑星と太陽とを結ぶ線分が単位時間に描く面積（面積速度）が一定であることを、膨大な観測データから導きましたが、この面積も、「微集積法」によって求められました。

イタリアの数学者ガヴァリエリ（1598年から1647年）は、平面を無限個の線分に分けることで、また、立体を無限個の面に分けることで、様々な図形の面積や体積を求めました。

その他無数の学者たちの研究があり、その上にさらなる研究が積み重ねられ続けてきたのです。

「微分」という概念とはまったく無関係に、微集積法があったのです。

ちなみに微集積法の $1$ つである区分求積法は、数学Ⅲにおいて学習します。
数学Ⅱまでしかやらない人にも、好奇心を満たしていただければと思いますので簡単に紹介します。

区分求積法

$y=f(t)$
$t=a$
$t=b$
$t$ 軸
で囲まれた部分の面積を $S_{ ab }$ とします。
つまり、 $S_{ ab }$ は定数です。

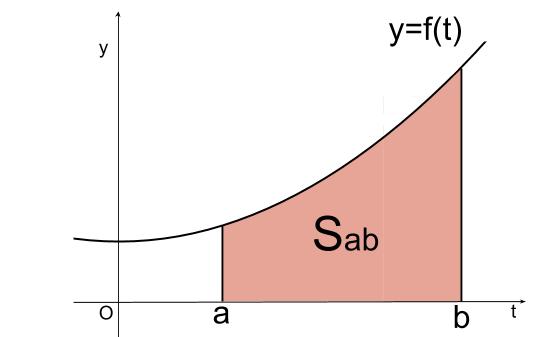
いわゆる「積分」の発見以前は、以下のように面積 $S_{ ab }$ を求めていました。

$a$ から $b$ の間を $n$ 等分して、長方形をしきつめます。
$n\longrightarrow \infty$ として、長方形の幅を限りなく細くすると、その和は
$S_{ ab }$ となる、これが古来からの求積のアイデアです。
※本当はもう少し厳密にやりますが、このページはコラムなので。

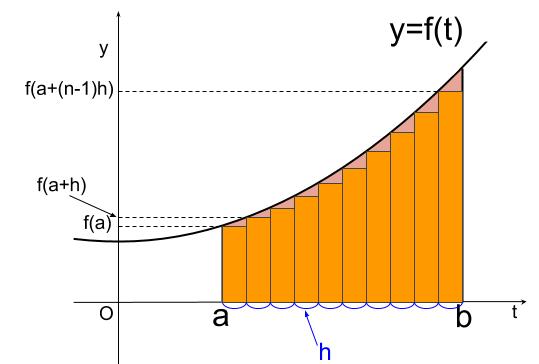
では、面積を求めましょう。
$\displaystyle \frac{b-a}{n}=h$ とします。
※$b-a \gt 0$ としましょう。

つまり、横幅は $h$、 高さは、 $f(a),f(a+h),f(a+2h),$・・・$,f(a+(n-1)h)$
の $n$ 個の長方形でしきつめられます。

$n$ 個の長方形の面積の和は、

$hf(a)+hf(a+h)+hf(a+2h)+$・・・$+hf(a+(n-1)h)=h \displaystyle \sum_{ k = 0 }^{ n-1 }f(a+kh)$

ここで、 $n\longrightarrow \infty$ として、長方形の幅を限りなく細くすると、その和は
$S_{ ab }$ となるので、

$S_{ ab }=\displaystyle \lim_{ n \to \infty } h \displaystyle \sum_{ k = 0 }^{ n-1 }f(a+kh)$

$\displaystyle \frac{b-a}{n}=h$ を使って表すと

$S_{ ab }=\displaystyle \lim_{ n \to \infty } \displaystyle \frac{b-a}{n}\displaystyle \sum_{ k = 1 }^{ n-1 } f(a+\displaystyle \frac{b-a}{n}k)$

これは無限級数の和になります。
数学Ｂで数列の学習をしていれば、具体的に計算可能です。
$f(x)=x^2$ とか、簡単な関数ならば、文系の高校生にもこの方法で面積が求められます。
より複雑な関数の面積をこの方法で求めるとなると、かなり大変であろうことが想像できれば十分です。

面積を求めることは、とても大変なことだったのです。

インテグラル記号の導入

さて「区分求積法」で苦労して求めた面積 $S_{ ab }=\displaystyle \lim_{ n \to \infty } \displaystyle \frac{b-a}{n}\displaystyle \sum_{ k = 1 }^{ n-1 } f(a+\displaystyle \frac{b-a}{n}k)$
ですが、この式の右辺はかなり複雑ですね。これを簡略化した表示方法が作られました。

$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{b-a}{n}\displaystyle \sum_{ k = 1 }^{ n } f(a+\displaystyle \frac{b-a}{n}k)=\displaystyle \int_a^b f(t) dt$

この式の右辺の意味は $a$ から $b$ までの区間で、$f(t)×dt$ という面積を足しあわせるという意味の式です。
$dt$ は$t$ 方向の変化量が超微小であることの表現であり、$\displaystyle \int$ は、$\displaystyle \sum$ の変形です。

この記号を作ったのはドイツの数学者ライプニッツ（1646年から1716年）で、和の英語(Sum) の S をたてに伸ばしてつくったそうです。
インテグラル $\displaystyle \int$ は、$\displaystyle \sum$ 同様、和の記号なのです。

さて、$a$ から $b$ までの区間で、$f(t)×dt$ という面積を足しあわせると定数が求まりますが、$b$ を変数 $x$ にしてみましょう。

$a$ から $x$ までの区間で、$f(t)×dt$ という面積を足しあわせると、$x$ の値しだいで、求まる面積が決まる $x$ の関数が得られます。この面積の関数を $S_{ a }(x)$ とします。

例えば、
$a$ から $x=10$ までの区間の面積は、$S_{ a }(10)$
$a$ から $x=20$ までの区間の面積は、$S_{ a }(20)$
ということです。

これはライプニッツの表記にしたがえば、

$S_{ a }(x)=\displaystyle \int_a^x f(t) dt$

です。

繰り返しになりますが、おなじみの記号、$\displaystyle \int$ は「微分の逆」ではないですよ。$\displaystyle \sum$ 同様、和の記号なのです。

２．微分

接線の傾きを求めるという微分係数の考え方も、古くから知られていたようです。

また、「微小な変化率」の研究も様々な時代、様々な地域で行われていたようです。

「微小な変化率」の研究の代表例は、「落下する物体の位置」と「その物体の瞬間の速度」の関係です。これは、「大砲の玉をいかに的確に命中させるか」という研究と直結していました。あるいは、「惑星の動き」の研究です。

例えば物体が落下していくときの、瞬間の速さ。
鉄球を、下り坂で転がし、時間と位置を観測する実験をします。

$1$ 秒後に $0.5m$
$2$ 秒後に $2m$
$3$ 秒後に $4.5m$ 地点にいたことは測れました。

この観測データから、位置 $L$ は、時間 $t$ と 比例定数 $a$ を用いて

$L=at^2$

と表せそうです。上の実験ならば、$a=0.5$ ですね。
※下り坂の傾きしだいで比例定数は変わります。

さて、刻一刻と速さを増して転がり落ちていく鉄球ですが、$3$ 秒後の、まさにその瞬間の秒速は一体どうやって求めたらいいのでしょうか？

$L=0.5t^2$
という関数を、時間 $t$ で微分ですると、速さ $v$ が求まることが研究されました。
$L=at^2$ から
$v=2at$ が導かれます。

微分はこのような研究につながっていました。

当然ですが、
速さと時間の関数、$v=2at$ から、微分する前の関数を求めることも研究されました。
微分する前の関数、つまり「原始関数」を求めるということです。
この操作は「逆微分」とでも呼ぶことにしましょう。
「逆微分」もこのコラム限定の言葉です。

「逆微分」が面積を求めることに結びつくなど、ぜんぜん自明のことではありませんね。
※注！！
現代の高校生は、この「原始関数」を求めることを「積分」と習ったわけですね・・・
微分の逆は「積分」という予備知識は捨ててください。あなたはまだ「積分」を知りません。

３．微分と積分の融合

そして「微分」や「微集積法」が研究され、先人の研究の上にさらに研究が積み重ねられ・・・
ついに $17$ 世紀、ヨーロッパの数学者たちが、「微分」と「微集積法」が互いに関連していることを発見しました。

筆者は、誰がいつ、どのような方法でこれを証明したのかはわかりません。だれがはじめてだったのかもわかりません。当時の数学者たちの表記は、現代とは違いますし、現代のように理論が整えられる前段階での研究です（幾何学がメインだったそうです）。また、同じような発見が同時多発的に出現することも普通です。これについて、数学史的に完全な記述をすることは、筆者の能力を超えています。

筆者の狙いは、「微分積分学の基本定理って人類にとって大発見だったんだ！」ということを伝えることです。ですので、発見の経緯や背景、その他もろもろ、年代の前後などが数学史的に正しくないことも多いでしょうが、教育的フィクションと思っていただければと思います。上記の物理学への応用も、数学的に整備された後に行われたものかもしれません。どちらが先なのか筆者はわかりません。

さて、微分と積分を「微分積分学」としてまとめたはじめての人は、イングランドの数学者ニュートン（1643年から1727年）、ドイツの数学者ライプニッツ（1646年から1716年）であるといわれています。
それぞれ独立に行った仕事です。ほぼ同時期にまったく独立に達成されたということからも、天才がパッと閃いたのではなく、先人たちの積み重ねの上を進んでいけば必然的に辿りつく仕事であったことがうかがえます。
※ニュートンやライプニッツはまぎれもなく天才ですよ、念のため。天才だからこそ辿りつけたのです。

微分積分学の基本定理へ

さて、$17$ 世紀、ヨーロッパで、$f(x)$ の原始関数と面積 $S_{ a }(x)$ が関連していることが発見がされました。

$S_{ a }(x)=F(x)-F(a)$ が発見されたのです。

なぜ$f(x)$ の「逆微分」で原始関数を求めると、面積につながるのか。
なぜ面積 $S_{ a }(x)$ を微分すると、$f(x)$ になるのか。
これの理由は別ページにて解説しています。
この点が、最も不思議で面白い話題ですので、ぜひご一読ください。

さて、今までの話をまとめます。

事実１：面積 $S_{ a }(x)$ は区分求積法で求めていた。

$S_{ a }(x)=\displaystyle \lim_{ n \to \infty } \displaystyle \frac{x-a}{n}\displaystyle \sum_{ k = 1 }^{ n-1 } f(a+\displaystyle \frac{x-a}{n}k)=\displaystyle \int_a^x f(t) dt$

事実２：$f(x)$ の原始関数と面積 $S_{ a }(x)$ が関連している。

$S_{ a }(x)=F(x)-F(a)$

この $2$ つをあわせると

$\displaystyle \int_a^x f(t) dt=F(x)-F(a)$

(左辺)は区分求積の計算
(右辺)は「逆微分」の計算
まったく異なる $2$ つが結びついたことを表す式です。感動もんです！

両辺を微分すると、

$\displaystyle\frac{ d }{ dx } \displaystyle \int_a^x f(t) dt=f(x)$

これこそが「微分積分学の基本定理」ですね。

ところで「微分積分学の基本定理」は左辺を書き換えると
$\displaystyle\frac{ d }{ dx } \displaystyle \lim_{ n \to \infty } \displaystyle \frac{x-a}{n}\displaystyle \sum_{ k = 1 }^{ n-1 } f(a+\displaystyle \frac{x-a}{n}k) = f(x)$

のことですからね。

超訳すると、「区分求積法」で苦労して求めた左辺（面積の関数）を微分すると、もとの $f(x)$ に戻っちゃった！！

ということです。

不思議じゃないですか？

あまり不思議な気持ちがしない人は、「面積の関数を微分すると」の箇所をよく考えてみてください。

微分するっていうことは、$\displaystyle\frac{ d }{ dx } x^n=nx^{n-1}$ っていう魔法のように簡単な記号操作のことじゃないですよ。$f(x)=\sin x$ でもいいし、$f(x)=\log_{ 2 } x$ でもいいんです。

$S(x)$ を微分するということは、

$S'(x)=\displaystyle \lim_{ h \to 0 } \displaystyle \frac{S(x+h)-S(x)}{h}$

という計算をすることです。

これが区分求積の数列の和と逆操作だなんて、とても不思議じゃないですか！！

定積分と不定積分

「区分求積法」で苦労して求めてきた面積ですが、もはやその苦労はいりません。
面積を求めるためには「逆微分」です。

$S_{ a }(x)=F(x)-F(a)$ であることわかったからです。

$\displaystyle \int_{a}^x f(t) dt =F(x)-F(a)$ なので、

インテグラル $\displaystyle \int$ は、この「原始関数の差によって求積する計算方法の記号」として定着しています。原始関数を求める計算とはすなわち、「逆微分」です。

この操作を「積分」と呼ぶことにしましょう。

$x$ を定数 $b$ にしてこの計算をすると、$a$ から $b$ までの実際の面積が定数として求まります。これを定積分といいます。

$\displaystyle \int_{a}^b f(t) dt$ です。

$x$ のままこの計算をすると、$x$ の関数が得られます。定まった値が得られません。
これを不定積分といいます。このとき、下端の定数 $a$ が不定でも議論・計算に影響はありません。積分定数が変化するだけだからです。

$\displaystyle \int f(x) dx=F(x)+C$ （$C$ は積分定数）

このように、計算記号が整備されていきました。

まとめ

「微分積分学の基本定理」を再掲します。

左辺の、$\displaystyle \int_a^x f(t) dt$ を $\displaystyle \sum$ と思って見てみてください。無限級数の和を微分すると、もとの関数にもどる。
不思議ですね。

微分積分学の基本定理は、微分と積分は互いに逆演算であることを主張します。

繰り返しになりますが、歴史的には、このページのコラムのように話が進んだということはありません。紆余曲折して研究が進んでいきました。

演算記号は、多数の発明者がそれぞれに作り、多くの人に流通するようになったものが
今に残っているわけで、歴史的にはじめから上のような現代の記号で統一して話が進んでいったわけではありません。