微分の利用・不等式の証明

不等式の証明

(左辺) $\gt$ (右辺)の不等式の証明は　　
(左辺)－(右辺) $=f(x)$
とし
$f(x)$ の最小値 $\gt 0$ を示せばよい。

$x \geqq 0$ のとき、不等式 $x^3+4 \geqq 3x^2$

が成り立つことを証明しなさい。また、等号が成り立つのはどのようなときか求めなさい。

$f(x)=x^3+4-3x^2$ とすると

$f´(x)=3x^2-6x$
$=3x(x-2)$

$f´(x)=0$ のとき $x=0,2$

$x \geqq 0$ の範囲で増減表とグラフは次のようになる。

$\begin{array}{c|ccccc}
x & 0 & \cdots & 2 & \cdots \\
\hline
f´(x) & 0 & – & 0 &+& \\
\hline
f(x) & 4 & \searrow & 0 & \nearrow \end{array}$

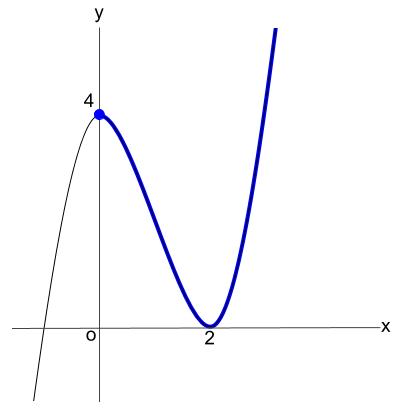
$高校数学無料学習サイトko-su- 微分不等式の証明1$

グラフより、$x \geqq 0$ のとき、$f(x) \geqq 0$であるから
$x^3+4x-3x^2 \geqq 0$
つまり、
$x^3+4 \geqq 3x^2$

また、等号成立は、 $x=2$ のとき。
グラフから明らかですね。

$x \gt 0$ のとき、不等式 $x^3-3x^2+4x+1 \gt 0$

が成り立つことを証明しなさい。

$f(x)=x^3-3x^2+4x+1$ とすると

$f´(x)=3x^2-6x+4$

$D \lt 0$ より、

$f´(x)=0$ となる $x$ は存在しないため、
増減表は次のようになる。

$\begin{array}{c|ccccc}
x & \cdots \\
\hline
y’ & +& \\
\hline
y & \nearrow \end{array}$

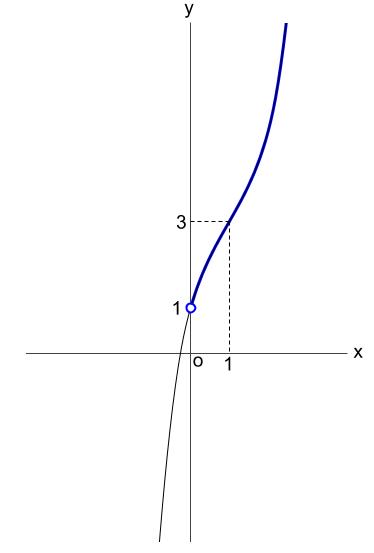
$高校数学無料学習サイトko-su- 微分不等式の証明2$

グラフより、$x \gt 0$ のとき $f(x) \gt 0$ であるから、
$x^3-3x^2+4x+1 \gt 0$
が成り立つ。

$f´(x)=3x^2-6x+4$
$=3(x-1)^2+1$
なので、
$f´(x)=3x^2-6x+4$ のグラフの頂点の $x$ 座標は $x=1$
この $x=1$ が変曲点の$x$ 座標となります。