３次方程式の解

\(3\) 次方程式 \(f(x)=0\) の解は、
\(y=f(x)\) のグラフと \(x\) 軸との共有点の \(x\) 座標である。
※\(2\) 次方程式のときと同様ですから、あたりまえですね！

ですから、
\(3\) 次方程式 \(f(x)=0\) の異なる実数解の個数は、　　
\(y=f(x)\) のグラフと \(x\) 軸との共有点の個数と一致します。

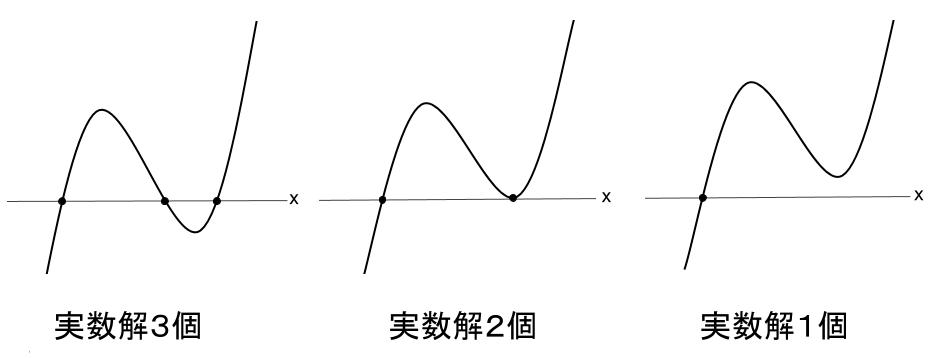
図からも明らかなのですが、\(3\) 次方程式の場合、「実数解なし」というケースはありません。

例題１

次の方程式について、異なる実数解の個数を求めなさい。

\(x^3-6x^2+9x-1=0\)

解説

\(f(x)=x^3-6x^2+9x-1\) とすると

\(f´(x)=3x^2-12x+9\)
\(=3(x-1)(x-3)\)

\(f´(x)=0\) のとき \(x=1,3\)

\(\begin{array}{c|ccccc}
x & \cdots & 1 & \cdots & 3 & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 3 & \searrow & -1 & \nearrow\end{array}\)

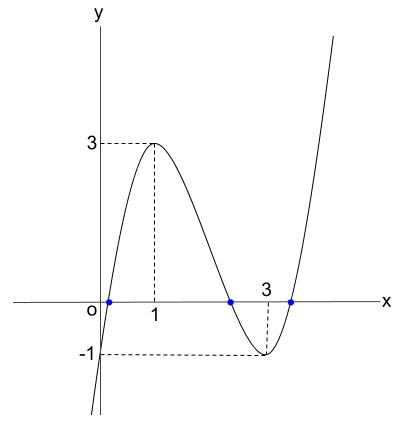
よって、グラフより異なる実数解を \(3\) つもつ。

※青丸の \(x\) 座標は、本問では聞かれていません。
この\(x\) 座標のとき、\(x^3-6x^2+9x-1=0\) が成り立つわけですね。
この \(x\) を求めることを、\(3\) 次方程式を解く、というわけです。

例題２

次の方程式について、異なる実数解の個数を求めなさい。

\(-x^3+3x^2-4=0\)

解説

\(f(x)=-x^3+3x^2-4\) とすると

\(f´(x)=-3x^2+6x\)
\(=-3x(x-2)\)

\(f´(x)=0\) のとき \(x=0,2\)

\(\begin{array}{c|ccccc}
x & \cdots & 0 & \cdots & 2 & \cdots \\
\hline
f’(x) & – & 0 & + & 0 & – \\
\hline
f(x) & \searrow & -4 & \nearrow & 0 & \searrow\end{array}\)

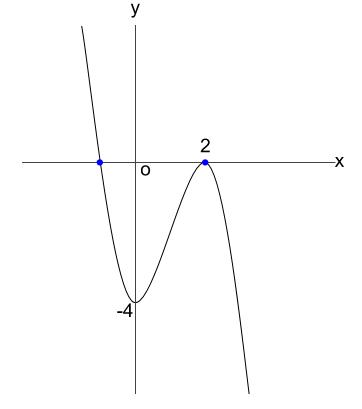
よって、グラフより異なる実数解を \(2\) つもつ。