余弦定理

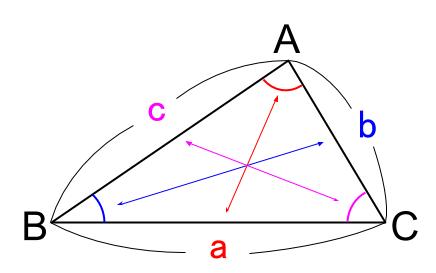
$\triangle ABC$ において、以下の式が成り立ちます。
これを余弦定理といいます。

$a^2=b^2+c^2-2bc \cos A$
$b^2=c^2+a^2-2ca \cos B$
$c^2=a^2+b^2-2ab \cos C$

$3$ つの式はいずれも対称的になっていますね。
$a$ からはじまる式にでてくる角は、対角の $A$ です。

※内角の $1$ つか鈍角のときも、余弦定理は成り立ちます。
※三平方の定理 $c^2=a^2+b^2$ に、微調整をしているのが余弦定理です。

なぜこれが成り立つのか、は別ページに譲ります。
この定理をどのように用いるのか、まずは例題演習をしましょう。

例題１

次のような三角形 $ABC$ において、指定されたものを求めなさい。

$b=4,c=\sqrt{3},A=30°$ のとき、長さ $a$

解説

ここで余弦定理の最重要ポイントです！

わかっている角か、求めたい角の対辺からはじまる式を用います。

暗記してくださいね。

では解きましょう。
$b=4,c=\sqrt{3},A=30°$ のとき、長さ $a$ です。

分かっている角は $A$ なので、その向かいの辺 $a$ からはじまる式です。

$a^2=4^2+(\sqrt{3})^2-2×4×\sqrt{3}× \cos 30°$

$a^2=16+3-2×4×\sqrt{3} ×\cos 30°$

$\cos 30°=\displaystyle \frac{\sqrt{3}}{2}$ なので、

$a^2=7$
$a=\pm \sqrt{7}$

$a$ は $0$ より大きいので、

$a=\sqrt{7}$

ちなみに、$2$ 辺とその間の角が与えられていますので、
三角形は $1$ つに定まります。
いわゆる三角形の合同条件ですね。

三角形が $1$ つに定まらない問題もあり、
$2$ つの答えがでるようなものもあります。

例題2

次のような三角形 $ABC$ において、指定されたものを求めなさい。

$a=1,b=\sqrt{2},c=\sqrt{5}$ のとき、角 $C$

解説

求めたい角 $C$ の向かいの辺 $c$ からはじまる式です。

$(\sqrt{5})^2=1^2+(\sqrt{2})^2-2×1×\sqrt{2} × \cos C$

$5=1+2-2\sqrt{2}× \cos C$

$2\sqrt{2}× \cos C=-2$

$\cos C=-\displaystyle \frac{1}{\sqrt{2}}$

よって、
$C=135°$

ちなみに、$3$ 辺が与えられていますので、
三角形は $1$ つに定まります。
いわゆる三角形の合同条件ですね。

例題３

次のような三角形 $ABC$ において、指定されたものを求めなさい。

$a=1,b=\sqrt{3},A=30°$ のとき、長さ $c$

解説

分かっている角は $A$ なので、その向かいの辺 $a$ からはじまる式です。

$1^2=c^2+(\sqrt{3})^2-2×\sqrt{3}×c× \cos 30°$

$1=c^2+3-2×1×\sqrt{3} ×c×\cos 30°$

$\cos 30°=\displaystyle \frac{\sqrt{3}}{2}$ なので、

$c^2-3c+2=0$

$(c-1)(c-2)=0$

$c=1,2$

あれ、答えが $2$ つでてきた・・・
どっちかは不適かな？

ちなみにどちらもＯＫです。
はじめに与えられたものが 「$2$ 辺の長さ」と「その間でない角の大きさ」だったわけです。
中学のときに学習した三角形の合同条件ではありませんね。
つまり、三角形が $1$ つに定まらない条件だったわけです。

別解

余弦定理で解いたこの例題 $3$ は、
実は正弦定理でも解答可能です。

$a=1,b=\sqrt{3},A=30°$ のとき、長さ $c$ です。
正弦定理でいってみましょー！

$\displaystyle \frac{1}{\sin 30°}=\displaystyle \frac{\sqrt{3}}{\sin B}$

$\sin B=\displaystyle \frac{\sqrt{3}}{2}$

$B=60°,120°$

あれ、どちらがは不適なのかな？
どちらもＯＫです。

この続きは、
正弦定理でも
余弦定理でも
求められますが、図示してしまうのも早いです。

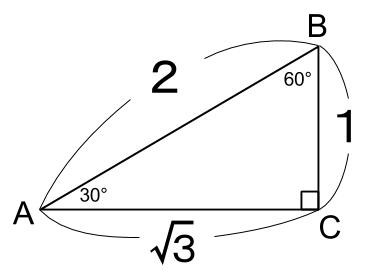
$B=60°$ のとき

$A=30°$ が与えられているので、三角形の内角より、$C=90°$ なので、これを用いて
$c=2$ が求まります。
三角定規型です。

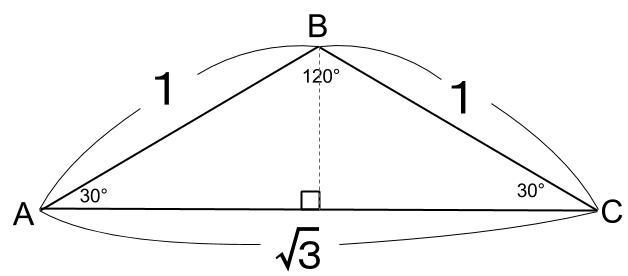
$B=120°$ のとき

$A=30°$ が与えられているので、三角形の内角より、$C=30°$ なので、これを用いて
$c=1$ が求まります。
$30°,60°,90°$ の三角定規 $2$ つ分の二等辺三角形になります。

Copyright secured by Digiprove © 2019 ko-su- info