方べきの定理
方べきの定理
3つのケースがある。
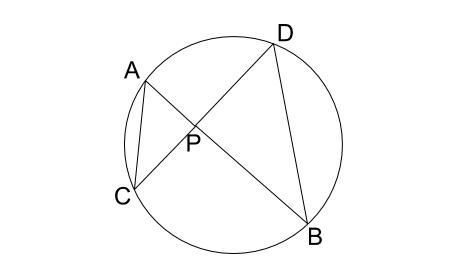
1.点 \(P\) が円の内部にあるとき
\(PA \cdot PB=PC \cdot PD\)
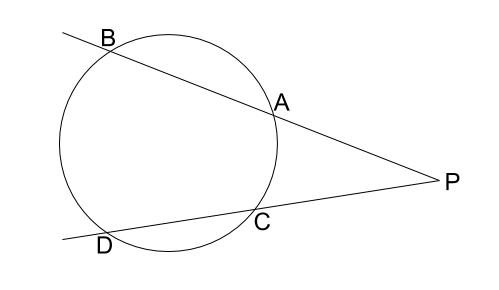
2.点 \(P\) が円の外部にあるとき
\(PA \cdot PB=PC \cdot PD\)
どちらのケースも、「点 \(P\)と円の交点までの距離」の積になっていて、非常に覚えやすい定理です。
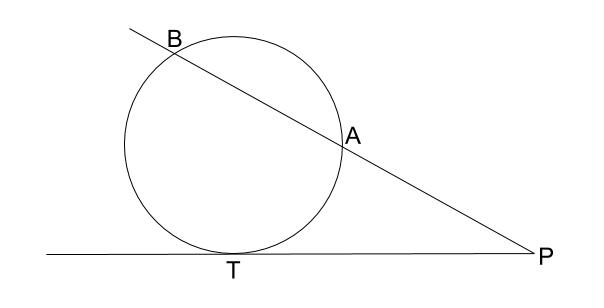
3.直線が円と接しているとき
\(PA \cdot PB=PT^2\)
点 \(T\) が重解のようになっています。
2つ目の場合の特殊ケースですね。
方べきの定理はなぜ成り立つのか。
いずれのケースも、三角形の相似から説明されます。
1.点 \(P\) が円の内部にあるとき
円周角の定理から、下図の赤い角、ピンクの角がそれぞれ等しいため、
クリーム色の三角形が相似です。
\(\triangle PAC \backsim \triangle PDB\)
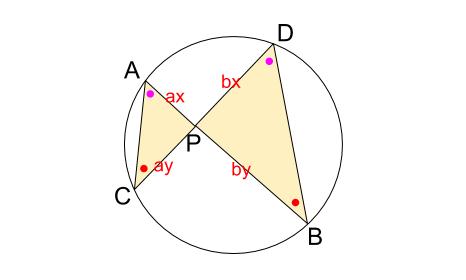
相似比が \(a:b\) のとき、
\(PA \cdot PB=ax\cdot by=abxy\)
\(PC \cdot PD=ay\cdot bx=abxy\)
より、\(PA \cdot PB=PC \cdot PD\)
2.点 \(P\) が円の外部にあるとき
円に内接する四角形の性質からピンク色の角が等しく、
\(\triangle PAC\) と \(\triangle PDB\) が相似です。
赤い角は共通です。\(2\) つの角が等しいので相似です。
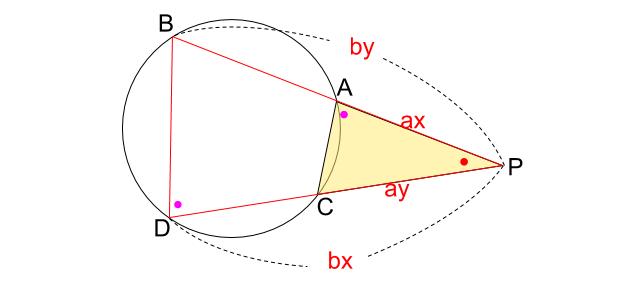
相似比が \(a:b\) のとき、
\(PA \cdot PB=ax\cdot by=abxy\)
\(PC \cdot PD=ay\cdot bx=abxy\)
より、\(PA \cdot PB=PC \cdot PD\)
3.直線が円と接しているとき
接弦定理より、下図のピンク色の角が等しく、
\(\triangle PAT\) と \(\triangle PTB\) が相似です。
赤い角は共通です。\(2\) つの角が等しいので相似です。
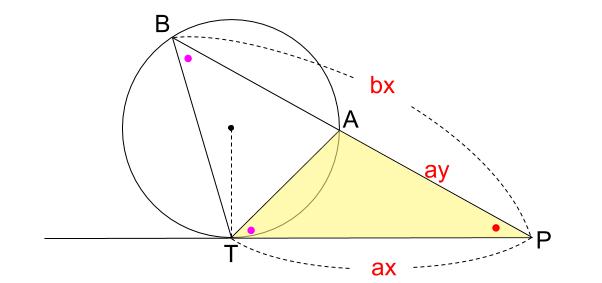
相似比が \(a:b\) とするとき、
\(\triangle PAT\) の辺 \(TP\) と \(\triangle PTB\) の辺 \(BP\)
が対応する辺なので、
\(TP=ax\)、\(BP=bx\)・・・①
とおけます。
また、\(\triangle PAT\) の辺 \(PA\) と \(\triangle PTB\) の辺 \(PT\)
が対応する辺なので、
\(PA=ay\) とおくと、\(TP=by\) とおけますが、①より
\(TP=ax=by\)・・・②
さて、方べきの定理が成り立っていることを確かめましょう。
\(PT^2=(ax)^2\)
\(PA \cdot PB=ay \cdot bx=abxy=ax \cdot by\)
②より、\(ax \cdot by=(ax)^2\)
よって、\(PA \cdot PB=PT^2\) が確かめられました。
例題1
下図の \(x\) を求めなさい。ただし、点 \(A\) は円と直線の接点です。
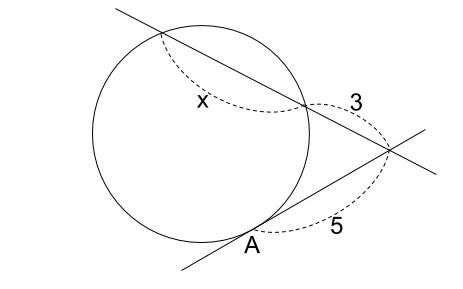
解説
方べきの定理より、
\(3(3+x)=5^2\)
\(3(3+x)=25\)
\(3+x=\displaystyle \frac{25}{3}\)
\(x=\displaystyle \frac{16}{3}\)
以上、求まりました。
例題2
下図の \(x\) を求めなさい。
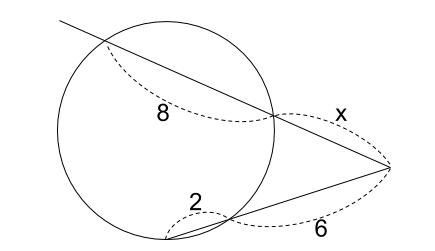
解説
方べきの定理より、
\(x(x+8)=6(6+2)\)
\(x^2+8x=48\)
\(x^2+8x-48=0\)
\((x-4)(x+12)=0\)
\(x=4,-12\)
\(x\) は正なので
\(x=4\)
以上、求まりました。
例題3
下図の \(AB\)、\(CE\) の長さを求めなさい。

解説
方べきの定理より、
\(EA \cdot EC=EB \cdot ED\) なので、
\(2×EC=4 \cdot 6\)
より、\(EC=12\)
また、\(\triangle EAB\) と \(\triangle EDC\) が相似で、
相似比は、\(EA : ED =2:6=1:3\)
\(AB:DC=1:3\) なので、
\(AB=DC ×\displaystyle \frac{1}{3}=5\)
以上求まりました。