常用対数の利用(放射性元素・バクテリア)
常用対数の利用
現実世界おいて、どのように対数が利用されているのか。
その一部を実感できる文章題です。
現実の世界の中に、指数、対数が溢れています。
例題1
一定の比率で崩壊し、\(8\) 日たつと量が半分になる放射性元素がある。
この放射性元素が初めの量の \(\displaystyle \frac{1}{10}\) になるのは何日後か。
ただし、\(\log_{ 10 } 2=0.3010\) として計算しなさい。
解説
\(2011\) 年の原発事故でも話題になった放射性元素についてです。
さて、一定の比率で崩壊するとあります。
はじめに \(100\) あったとして、\(8\) 日たつと \(50\) になります。
さらに \(8\) 日たつと・・・
\(50\) の半分、\(25\) になるのです。
決して、 \(8\) 日たつと \(50\) に減り、さらに \(8\) 日たつと \(0\) になるわけではありません(この場合は、一定の速さで崩壊)。
一定の比率で崩壊とは、
\(8\) 日たつと \(\displaystyle \frac{1}{2}\)
\(16\) 日たつと \(\displaystyle \frac{1}{4}\)
\(24\) 日たつと \(\displaystyle \frac{1}{8}\)
\(32\) 日たつと \(\displaystyle \frac{1}{16}\)
このような減り方をします。
これってつまり、指数関数なんです。
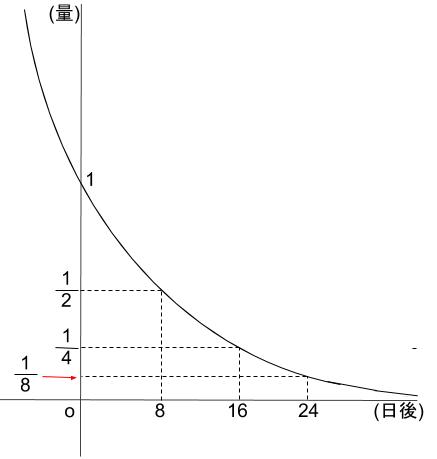
ところで、
\(\displaystyle \frac{1}{10}\) になるのは、\(26,27,28\) 日後あたりな気がしますね。
では、きちんと計算して求めていきましょう。
解答
\(1\) 日後に \(\displaystyle \frac{1}{n}\) になるとします。
すると、
\(2\) 日後に \((\displaystyle \frac{1}{n})^2\) になります。
\(3\) 日後に \((\displaystyle \frac{1}{n})^3\) になります。
\(x\) 日後に \((\displaystyle \frac{1}{n})^x\) になります。
問題の放射性元素は \(8\) 日たつと量が半分なるので、
\(8\) 日後には \((\displaystyle \frac{1}{n})^8=\displaystyle \frac{1}{2}\)
さあ、常用対数をとりましょう。
\(\log_{ 10 } (\displaystyle \frac{1}{n})^8=\log_{ 10 } \displaystyle \frac{1}{2}\)
\(8\log_{ 10 } \displaystyle \frac{1}{n}=\log_{ 10 } 1-\log_{ 10 } 2\)
\(8\log_{ 10 } \displaystyle \frac{1}{n}=0-0.3010\)
\(\log_{ 10 } \displaystyle \frac{1}{n}=\displaystyle \frac{-0.3010}{8}\)・・・①
さて、今我々が知りたいのは
\(x\) 日後に
\((\displaystyle \frac{1}{n})^x = \displaystyle \frac{1}{10}\)
ここも常用対数をとりましょう。
\(\log_{ 10 } (\displaystyle \frac{1}{n})^x = \log_{ 10 } \displaystyle \frac{1}{10}\)
\(x\log_{ 10 } \displaystyle \frac{1}{n} = -1\)
ここで①より、
\(\displaystyle \frac{-0.3010}{8}x = -1\)
\(x = \displaystyle \frac{8}{0.3010}=26.5780\cdots\)
より、\(27\) 日後となります。
※\(24×0.5780=13.872\)(時間) なので、およそ \(26\) 日と \(13\) 時間 \(52\) 分後にこの放射性元素は半分になります。答えとしては、\(27\) 日後のことですから、\(27\) 日後と答えます。
例題2
\(40\) 分ごとに個体数が\(2\) 倍になる割合で分裂をし続けるバクテリアがいる。このバクテリアが \(10^7\) 個以上に増えるのは、\(10\) 個であったときから何分後以降か。
ただし、\(\log_{ 10 } 2=0.3010\) とし、答えは整数で求めなさい。
解説
\(1\) 分で \(n\) 倍になるとします。
\(40\) 分で \(2\) 倍になるとは
\(n^{40}=2\)
ここで常用対数をとりましょう。
\(\log_{ 10 } n^{40} = \log_{ 10 } 2\)
\(40\log_{ 10 } n = \log_{ 10 } 2\)
\(\log_{ 10 } n = \displaystyle \frac{\log_{ 10 } 2}{40}\)
\(\log_{ 10 } n = \displaystyle \frac{0.3010}{40}\) ・・・①
また
\(M\) 分後に \(10^7\) 個以上になったならば
\(10×n^M \geqq 10^7\)
ここで常用対数をとると
\(\log_{ 10 } (10×n^M) \geqq \log_{ 10 } 10^7\)
\(\log_{ 10 } 10+ \log_{ 10 } n^M \geqq \log_{ 10 } 10^7\)
\(\log_{ 10 } 10+ M\log_{ 10 } n \geqq \log_{ 10 } 10^7\)
\(1+ M\log_{ 10 } n \geqq 7\)
①より、
\(1+ M×\displaystyle \frac{0.3010}{40} \geqq 7\)
\(M×\displaystyle \frac{0.3010}{40} \geqq 6\)
\(M \geqq \displaystyle \frac{6×40}{0.3010} \)
\(M \geqq 797.342\cdots\)
よって \(798\) 分後以降です。