三角関数の相互関係
三角関数の相互関係
\(\sin^2 \theta +\cos^2 \theta =1\)
\(\tan \theta=\displaystyle \frac{\sin \theta}{\cos \theta}\)
\(\tan^2 \theta+1=\displaystyle \frac{1}{\cos^2 \theta}\)
数学Ⅰでは三角比の相互関係として学習しましたね。
これらは \(\theta\) がいくつであっても成立します。
「三角比」なのか「三角関数」なのか、どっちでもよろしい。
つまり、あらゆる一般角に対して成立します。
とても覚えやすくてうれしいですね。
例題1
\(\theta\) の動径が第 \(4\) 象限にあり、\(\sin \theta =-\displaystyle \frac{1}{4}\)のとき、
\(\cos \theta\)、\(\tan \theta\) の値を求めなさい。
解説
第 \(4\) 象限がどこかわからないってことはないですよね。
一応確認です。座標平面を \(4\) つにわけます。
\(\sin \theta\) は 単位円周上での \(y\) 座標です。
簡単に図示しましょう。
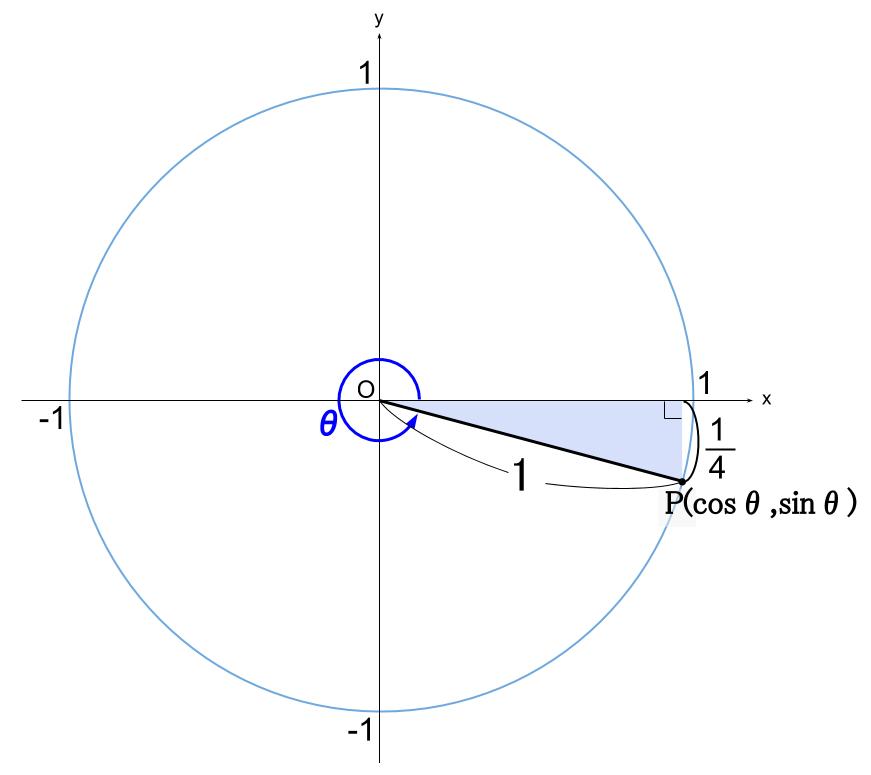
水色の直角三角形に三平方の定理を適用すれば
点 \(P\) の \(x\) 座標である、\(\cos \theta\) が求まります。
\((-\displaystyle \frac{1}{4})^2+ \cos^2 \theta =1^2\)
より、\(\cos^2 \theta=\displaystyle \frac{15}{16}\)
\(\cos \theta=\pm \sqrt{\displaystyle \frac{15}{16}}=\pm \displaystyle \frac{\sqrt{15}}{4}\)
\(\theta\) の動径が第 \(4\) 象限のとき、
\(\cos \theta \gt 0 \) なので、
\(\cos \theta = \displaystyle \frac{\sqrt{15}}{4}\)
これで求まりました。
三角関数の相互関係の式である、
\(\sin^2 \theta +\cos^2 \theta =1\)
を利用したのと同じ解き方です。
※そもそも \(\sin^2 \theta +\cos^2 \theta =1\) が水色の直角三角形の三平方の定理から得られるからです。
次に \(\tan \theta\) を求めましょう。
\(\tan \theta\) は直線 \(OP\) の傾きです。
つまり、\(\tan \theta=\) \(OP\) の傾き \(= \displaystyle \frac{yの増加量}{xの増加量}\)
です。中学 \(2\) 年生の一次関数のおさらいです。
よって、\(\tan \theta=\displaystyle \frac{-\displaystyle \frac{1}{4}}{ \displaystyle \frac{\sqrt{15}}{4}}=-\displaystyle \frac{1}{\sqrt{15}}=-\displaystyle \frac{\sqrt{15}}{15}\)
これは、\(\tan \theta=\displaystyle \frac{\sin \theta}{\cos \theta}\) を用いて解いたのと同じことですね。
例題2
\(\theta\) の動径が第 \(3\) 象限にあり、\(\tan \theta =\displaystyle \frac{3}{2}\)のとき、
\(\cos \theta\)、\(\tan \theta\)の値を求めなさい。
解説
\(\tan \theta\) は直線 \(OP\) の傾きです。
傾き \(\displaystyle \frac{3}{2}\) の直線を図示しましょう。
\(x\) が \(2\) 増えると \(y\) が \(3\) 増えるような傾きです。
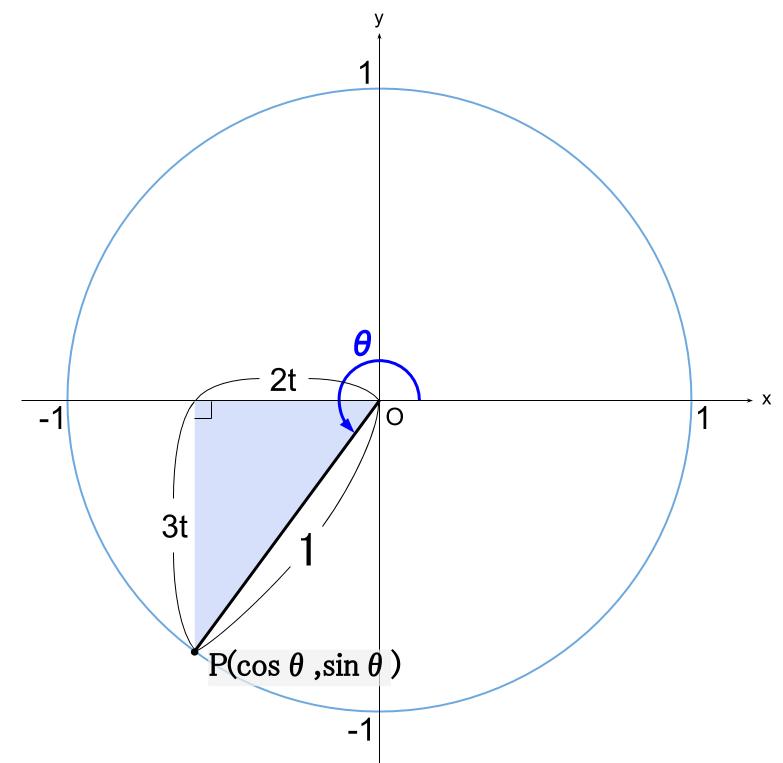
水色の直角三角形に三平方の定理を適用すれば
点 \(P\) の \(x\) 座標である、\(\cos \theta\) と
点 \(P\) の \(y\) 座標である、\(\sin \theta\) が求まります。
\((2t)^2+(3t)^2=1^2\)
より、
\(13t^2=1\)
\(t=\pm \sqrt{\displaystyle \frac{1}{13}}\)
\(t\) は直角三角形の長さであり、 \(t \gt 0\) よって
\(t= \sqrt{\displaystyle \frac{1}{13}}=\displaystyle \frac{\sqrt{13}}{13}\)
図より、
点 \(P\) の \(x\) 座標である、\(\cos \theta\) は\(-2t\)
よって、\(\cos \theta=-\displaystyle \frac{2\sqrt{13}}{13}\)
点 \(P\) の \(y\) 座標である、\(\sin \theta\) は\(-3t\)
よって、\(\sin \theta=-\displaystyle \frac{3\sqrt{13}}{13}\)