接線
接線
微分することで接線の傾きが求まる!!
とさんざん書いてきました。
ですので、接線を実際に求めていきましょう。
例題1
関数 \(y=2x^2-x+4\) のグラフ上の点 \((1,5)\) における接線の方程式を求めなさい。
解説
最終的には直線の方程式を求めることが目標です。
直線の方程式は \(y=ax+b\) ですね。
\(a\) が傾きです。
微分することで、傾き \(a\) がわかるわけです。
そして、通る点も与えられています。
通る点は式に代入です。
中学 \(2\) 年生の \(1\) 次関数のときからの定番です。
では問題を解きましょう!
\(f(x)=2x^2-x+4\)
\(f'(x)=4x-1\) なので、
\(f'(1)=3\)
つまり、グラフ上の点 \((1,5)\) における接線の方程式は
\(y=3x+b\) とおけます。
この直線は点 \((1,5)\) を通るので、\(y=3x+b\) に代入して、
\(5=3×1+b\)
より、\(b=2\)
よって、求める接線の方程式は \(y=3x+2\) です。
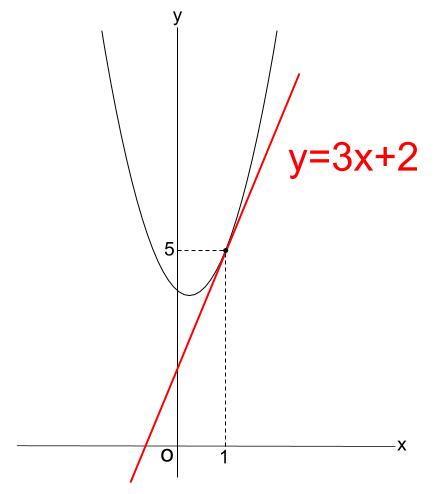
※参考図です。本問を解くさいに、作図は必要ありません。
例題2
\(y=x^3-5x^2+6x\) のグラフ上の点における接線の傾きが \(3\) のとき、
この接線の方程式を求めなさい。
解説
\(f(x)=x^3-5x^2+6x\) とすると、
\(f'(x)=3x^2-10x+6\)
\(f'(x)=3\) となる \(x\) を知りたいので、
\(3=3x^2-10x+6\)
この \(2\) 次方程式を解きます。
\(3x^2-10x+3=0\)
\((3x-1)(x-3)=0\)
より、
\(x=\displaystyle \frac{1}{3},3 \)
よって、\(y=x^3-5x^2+6x\) 上の点で \(x\) 座標が \(\displaystyle \frac{1}{3}\) と \(3\) のときに、
接線の傾きが \(3\) になることがわかりました。
\(x=\displaystyle \frac{1}{3},3 \) をそれぞれ \(y=x^3-5x^2+6x\) に代入して、
\((\displaystyle \frac{1}{3},\displaystyle \frac{40}{27})\) と \((3,0)\)
この \(2\) 点での接線を求めます。
\((\displaystyle \frac{1}{3},\displaystyle \frac{40}{27})\)
求める接線の傾きは \(3\) なので、その方程式は \(y=3x+b\) です。
\((\displaystyle \frac{1}{3},\displaystyle \frac{40}{27})\) を通るので、代入して
\(b=\displaystyle \frac{13}{27}\)
つまり、求める接線の方程式は \(y=3x+\displaystyle \frac{13}{27}\) です。
\((3,0)\)
求める接線の傾きは \(3\) なので、その方程式は \(y=3x+b\) です。
\((3,0)\) を通るので、代入して
\(b=-9\)
つまり、求める接線の方程式は \(y=3x-9\) です。
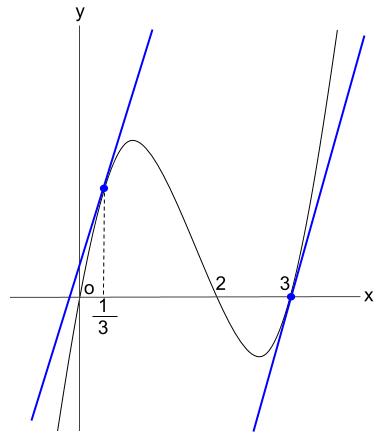
※参考図です。\(3\) 次関数のグラフはまもなく学習しますが、
点対称なグラフになります。
接線の傾きが同じになる点 \(2\) つも、点対称な位置にあります。
例題3
\(y=x^2-3\) のグラフに、点 \(P(1,-6)\) から引いた接線の方程式を求めなさい。
解説
接線の問題なので、導関数を用いるのでしょうね。
\(f(x)=x^2-3\) とすると、
\(f'(x)=2x\)
さて、グラフ上のどの点が接点となるかわからないので・・・
こういうときは文字でおく。
数学の鉄板解法ですね。
\(y=x^2-3\) のグラフに、点 \(P(1,-6)\) から引いた接線が
点 \((t,t^2-3)\) で接するとします。
※もちろん、点 \((t,t^2-3)\) における接線が、点 \(P(1,-6)\) を通るとも言えます。
点 \((t,t^2-3)\) における接線の傾きは
\(f'(t)=2t\)
なので、求める接線の方程式は
\(y=2tx+b\)
この直線は点 \((t,t^2-3)\) を通るので、代入して
\(t^2-3=2t×t+b\)
より、\(b=-t^2-3\)
よって、求める接線の方程式は
\(y=2tx-t^2-3\)
この接線は、点 \(P(1,-6)\) を通るので、代入して
\(-6=2t-t^2-3\)
この \(2\) 次方程式を解くと
\(t^2-2t-3=0\)
\((t+1)(t-3)=0\)
より、
\(t=-1,3\)
つまり、 \(y=x^2-3\) のグラフ上の点で \(x\) 座標が \(-1,3\) の点における接線が
求めるものになります。
\(x=-1,3\) を \(y=x^2-3\) に代入して、
\((-1,-2)\) と \((3,6)\)
この点での接線を求めます。
\((-1,-2)\)
求める接線の傾きは \(f'(-1)\) なので、
\(f'(x)=2x\) より、\(f'(-1)=-2\)
よって、接線の方程式は \(y=-2x+b\) です。
\((-1,-2)\) を通るので、代入して
\(b=-4\)
つまり、求める接線の方程式は \(y=-2x-4\) です。
\((3,6)\)
求める接線の傾きは \(f'(3)\) なので、
\(f'(x)=2x\) より、\(f'(3)=6\)
よって、接線の方程式は \(y=6x+b\) です。
\((3,6)\) を通るので、代入して
\(b=-12\)
つまり、求める接線の方程式は \(y=6x-12\) です。
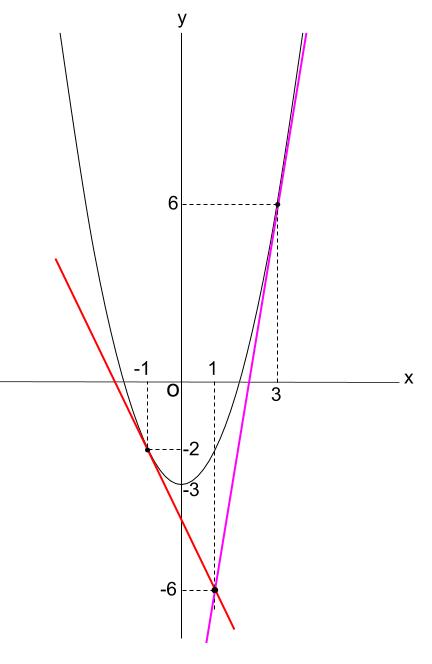
※参考図です。