3次関数と接線が囲む面積
3次関数と接線の囲む面積
接点の \(x\) 座標が \(\alpha\) 、交点の \(x\) 座標が \(\beta\) のとき、
\(S=\displaystyle \frac{|a|}{12}(\beta-\alpha)^4\)
※接点の \(x\) 座標が \(\beta\) 、交点の \(x\) 座標が \(\alpha\) のときも同一の公式でOK
裏ワザ公式を↑で紹介しておりますが、まずはまっとうにこの問題を解く力をつけましょう。
例題1
\(y=x^3-4x\) とその上の点 \((1,-3)\) における接線とで囲まれた部分の面積を求めなさい。
解説
接線の方程式を求めましょう。
\(y=x^3-4x\) より、\(y’=3x^2-4\)
\((1,-3)\) における接線は、\(y=-1\cdot(x-1)-3=-x-2\)
この接線と \(3\) 次関数 \(y=x^3-4x\) との交点の \(x\) 座標を求めます。
\(x^3-4x=-x-2\)
\(x^3-3x+2=0\)
これを因数分解するわけですが、\(x=1\) で接しているので、
必ず \((x-1)^2\) を因数に持ちます。
つまり、
\(x^3-3x+2=(x-1)^2(x-p)\) となります。
右辺を展開して、定数項 \(+2\) が出てくるので、
\(x^3-3x+2=(x-1)^2(x+2)\)
となることがわかります。
より、交点の \(x\) 座標は \(-2\)
また、\(y=x^3-4x=x(x+2)(x-2)\) なので、
大雑把にグラフをかくと下図のようになるでしょう。
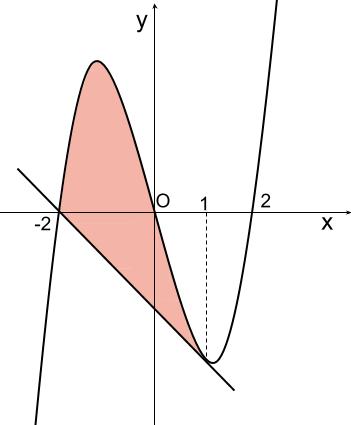
本問では、増減表をかいたり、極値を求める必要はありません。
では積分計算をしましょう。
\(S=\displaystyle \int_{-2}^1 \{(x^3-4x)-(-x-2)\} dx\)
\(=\displaystyle \int_{-2}^1 (x^3-3x+2) dx\)
\(=\left[\displaystyle \frac{1}{4}x^4-\displaystyle \frac{3}{2}x^2+2x \right]_{-2}^1\)
\(\begin{eqnarray}= & & \displaystyle \frac{1}{4}\{1^4-(-2)^4\} \\ &-& \displaystyle \frac{3}{2}\hspace{ 0pt }\hspace{ 1pt }\{1^2-(-2)^2\} \\ &+& \hspace{ 2pt }2\hspace{ 3pt }\{1\hspace{ 2pt }-(-2)\hspace{ 4pt }\} \end{eqnarray}\)
\(=\displaystyle \frac{27}{4}\)
ちょっと最後の計算が面倒ですが、特に工夫なしでも何とかなりますね。
ところで、この計算を楽に行う式変形のポイントがあります。
ポイント!積分のための式変形
\(S=\displaystyle \int_{-2}^1 \{(x^3-4x)-(-x-2)\} dx\)
\(=\displaystyle \int_{-2}^1 (x^3-3x+2) dx\)
さて、\(x^3-3x+2=(x-1)^2(x+2)\) です。
これはもともと接線 \(y=-x-2\) と \(3\) 次関数 \(y=x^3-4x\) との交点の \(x\) 座標を求めるときにおこなった計算です。
\(\displaystyle \int_{-2}^1 (x^3-3x+2) dx\)
\(=\displaystyle \int_{-2}^1 (x-1)^2(x+2) dx\)
※次が知らなきゃ思いつかない計算テクニックです。
\(=\displaystyle \int_{-2}^1 (x-1)^2\{(x-1)+3\} dx\)
※ \((x-1)\) を作り出します。
\(=\displaystyle \int_{-2}^1 \{(x-1)^3+3(x-1)^2\} dx\)
\(=\left[\displaystyle \frac{1}{4}(x-1)^4+3\cdot \displaystyle \frac{1}{3}(x-1)^3 \right]_{-2}^1\)
※公式、\(\displaystyle \int (x+b)^n dx=\displaystyle \frac{1}{n+1}(x+b)^{n+1}+C\) の利用
\(=0-\{\displaystyle \frac{1}{4}(-2-1)^4+(-2-1)^3\}=\displaystyle \frac{27}{4}\)
最後の代入のさいに、必ず片方が \(0\) になってくれるので計算は楽です。
ぜひ反復練習して身につけましょう。
参考
\(3\) 次関数と接線に囲まれた部分の面積 \(S\) は、
\(S=a\displaystyle \int_{\alpha}^{\beta} (x-\alpha)^2(x-\beta) dx\)
の形になります。
上の例題のように \((x-\beta)=\{(x-\alpha)+\alpha-\beta\}\) とすることで、
\(S=\displaystyle \frac{|a|}{12}(\beta-\alpha)^4\)
となることが計算できます。
これはいわゆる公式です。
\(2\) 次関数 \(ax^2+bx+c=0\) と、\(2\) 本の接線で囲まれた部分の面積 \(S\) は
接点の \(x\) 座標が \(\alpha,\beta\) のとき、
\(S=\displaystyle \frac{|a|}{12}(\beta-\alpha)^3\)
と似ています。
使用のさいは使い間違えることがないように!!