\(3\) 次関数のグラフをかく

我々の最大の目標は

\(3\) 次関数のグラフをかくこと！

です。

数学の初心者である高校生にとっては
「微分は \(3\) 次関数のグラフをかくために学習した」
と言ってしまってもいいくらいなのです。

※微分によって、さまざまな計算が可能になっている現代社会。
とりわけ微分方程式は、ありとあらゆる分野で必須の重要なツールですが、
微分方程式は高校数学では扱いません。

\(3\) 次関数のグラフの概形

\(3\) 次関数のグラフについて学習しますが、
まずはその概形を知りましょう。

\(y=ax^3+bx^2+cx+d\) に様々な数値を入れて、
\(x=0\) のときの \(y\)
\(x=1\) のときの \(y\)
などと、実際に計算をして、グラフが通る座標を求めていけば、
おおよそ以下のようなグラフになることが確かめられます。

\(0 \lt a\)

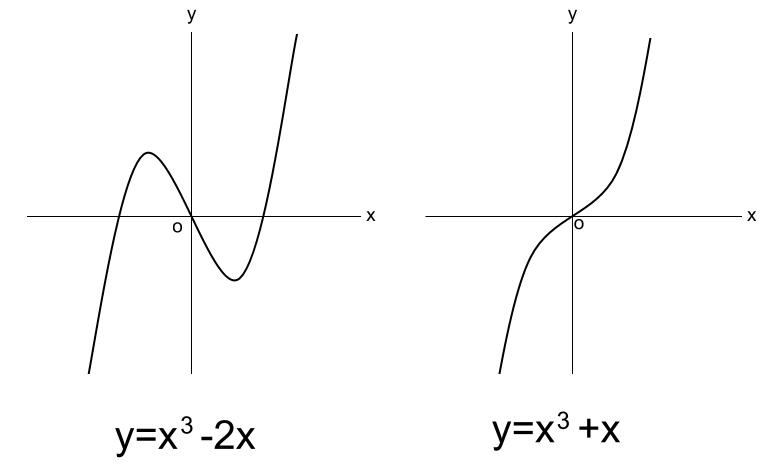
\(a \lt 0\)

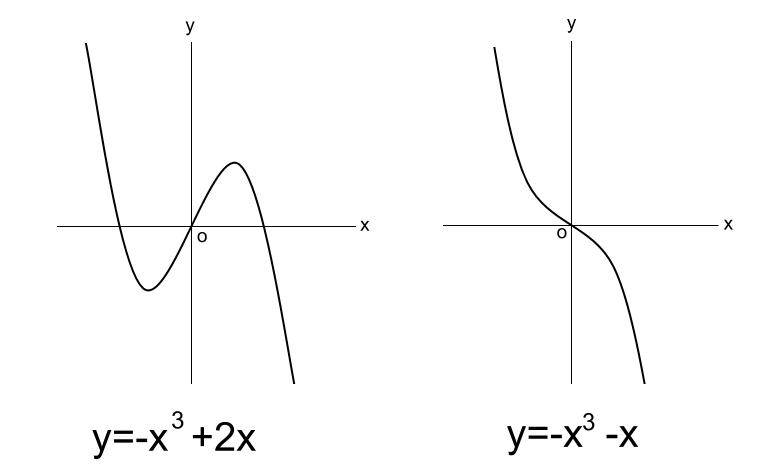
まずはこの概形を頭に入れてしまいましょう。

\(3\) 次関数のグラフはすべて点対称です。
上であげた例ではすべて、原点 \(O\) が対称の中心となっています。
もちろんグラフを平行移動すれば、対称の中心はずれます。

\(3\) 次関数のグラフの対称の中心は変曲点とよばれます。
極大値と極小値のちょうど中間地点が変曲点です。
対称の中心ですからね。

極大値と極小値は以下で説明します！

極大値・極小値

実際にみなさんが \(3\) 次関数のグラフをかくときに、
実際に座標をいくつもプロットしてかくということはしません。

\(2\) 次関数のグラフをかくときを思い出してください。
\(2\) 次関数のグラフの最大の特徴は、頂点でしたね。
頂点の位置を求めて、そのあとは上に凸か下に凸かで
概形をさらっとかけばOKでした。

\(3\) 次関数も似たようなものです。
グラフにおける山や谷の位置を求めて、曲線でつなぎます。
頂点ではなく、極値といいます。

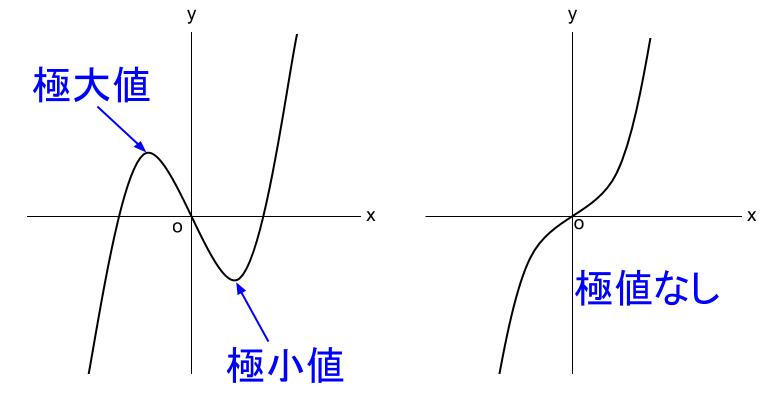
山の頂点の \(y\) 座標を極大値といいます。
谷の底の \(y\) 座標を極小値といいます。
極大値と極小値をまとめて、極値といいます。

極値はどうやって求めたらいいのでしょうか。
そして、極値を持たない場合もあるので、
その判定はどうしたらいいのでしょうか。

ずばり、微分なのです。

増減表・３次関数のグラフ

例
\(y=\displaystyle \frac{1}{3}x^3-\displaystyle \frac{1}{2}x^2-2x\)

この \(3\) 次関数のグラフをかいてみましょう。

まずは導関数です。
\(y’=x^2-x-2\)
\(=(x+1)(x-2)\)

導関数をみれば、もとの関数のグラフのおおよその概形がわかる、
前回学習したことです。

傾きが、正か負か \(0\) かのみに注目すればよいのです。
特に \(0\) が大事です。

導関数において、\(x\) を負の方向から正の方向へ、どんどん大きくしていってみましょう。

\(x \lt -1\) のときは、常に \(y’\gt 0\)
つまり、接線の傾きが正なのでもとのグラフは上り坂です。

\(x=-1\) になると接線の傾きが \(0\) 、つまりもとのグラフは平らになり、

\(x=-1\) をほんの少しでも超えると、\(y’\lt 0\) となります。
つまり、接線の傾きが負なのでもとのグラフは下り坂です。

\(y’\lt 0\)　なのは、、\(-1 \lt x \lt 2\) の範囲です。

\(x=2\) となると接線の傾きが再び \(0\) になります。つまりもとのグラフは平らになります。

\(x=2\) をほんの少しでも超えると、\(y’\gt 0\) となります。
つまり、接線の傾きが正なのでもとのグラフは上り坂です。

この情報は増減表というものにまとめるのが慣例です。

\(\begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 2 & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & \displaystyle \frac{7}{6} & \searrow & -\displaystyle \frac{10}{3} & \nearrow\end{array}\)

\(f(-1)=\displaystyle \frac{7}{6}\)　や \(f(2)=-\displaystyle \frac{10}{3}\) の値は、

\(f(x)=\displaystyle \frac{1}{3}x^3-\displaystyle \frac{1}{2}x^2-2x\)

に代入して計算して求めます。

さて、増減表から得た情報からグラフをかきます。

まずは極値をとります。
同じく増減表から、
増えて、減って、増えるグラフであることがわかるので下図のような概形です。

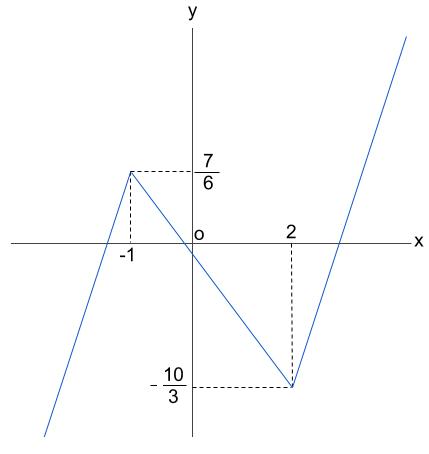
しかし、こんなにカクカクのグラフをかいてはいけません。
「\(3\) 次関数のグラフはおおよそこうなる」という知識をもとに、
なめらかにつなぐのが暗黙のルールです。

特に大事な \(2\) 点を挙げます。

極値では、傾きが \(0\) であること。
極値は、放物線の頂点のようにかきます。
だんだん傾きが緩やかになっていき、\(0\) になり、
まただんだん傾きが急になっていきます。

\(y\) 軸との交点も求める。
\(x=0\) のときの値はとても簡単に求められます。
必ず求めましょう。
\(x\) 軸との交点は、必ずしも求める必要はありません。

\(y=\displaystyle \frac{1}{3}x^3-\displaystyle \frac{1}{2}x^2-2x\) で \(x=0\) のとき \(y=0\)
よって、\(y\) 軸との交点は原点なので、グラフは下図のようになります。

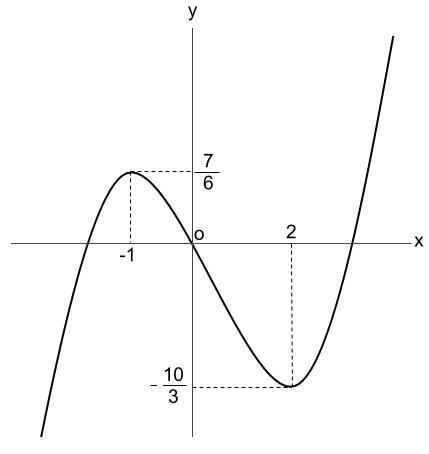
ちなみに変曲点（対称の中心）は、\(2\) つの極値の中間地点です。
つまり、 \(x=-1\) と \(x=2\) の中間、\(x=\displaystyle \frac{1}{2}\) の点です。
作図において、少し意識できると良いですが、あまりこだわらないでもＯＫです。

次ページで、さまざま \(3\) 次関数のグラフをかく練習を積んでいきましょう！