ポイント

$\sin \theta$ と $\cos \theta$ が混在している式は、
合成によって、$\sin (\theta+a)$ と $1$ つにまとめることが基本的な方針になります。

合成できるのは、角が同じときです。
$a\sin \theta$ と $b\cos \theta$ は合成できますが、
$a\sin \theta$ と $b\cos 2\theta$ は合成できません。

例題１

$0 \leqq \theta \lt 2\pi$ のとき、次の方程式 を解きなさい。
$\sin \theta-\cos \theta=1$

解説

角がどちらも $\theta$ なので、合成しましょう。

$\sin \theta-\cos \theta=1$

$\sqrt{2} \sin (\theta-\displaystyle \frac{\pi}{4})=1$
※あるいは、$\sqrt{2} \sin (\theta+\displaystyle \frac{7}{4}\pi)=1$ どちらでもＯＫです。

$\sin (\theta-\displaystyle \frac{\pi}{4})=\displaystyle \frac{1}{\sqrt{2}}$

$0 \leqq \theta \lt 2\pi$ のとき

$-\displaystyle \frac{\pi}{4} \leqq \theta-\displaystyle \frac{\pi}{4} \lt \displaystyle \frac{7}{4}\pi$

下図のようになります。

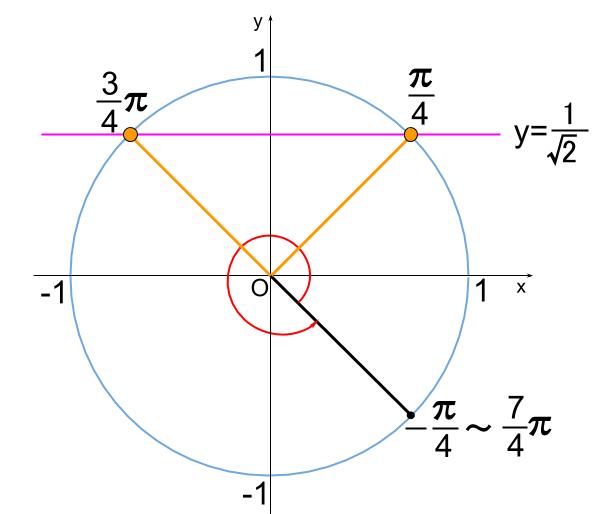
よって、$0 \leqq \theta \lt 2\pi$ のとき求める解は、
$\theta-\displaystyle \frac{\pi}{4}=\displaystyle \frac{\pi}{4}$ と　$\theta-\displaystyle \frac{\pi}{4}=\displaystyle \frac{3}{4}\pi$

よって、$\theta=\displaystyle \frac{\pi}{2},\pi$

例題２

$0 \leqq \theta \lt 2\pi$ のとき、次の不等式 を解きなさい。

$\sqrt{3}\sin \theta+\cos \theta \lt \sqrt{2}$

解説

角がどちらも $\theta$ なので、合成しましょう。

$\sqrt{3}\sin \theta+\cos \theta =2\sin(\theta+\displaystyle \frac{\pi}{6})$ と合成できるので、

$\sqrt{3}\sin \theta+\cos \theta \lt \sqrt{2}$　は

$2\sin(\theta+\displaystyle \frac{\pi}{6}) \lt \sqrt{2}$

$\sin(\theta+\displaystyle \frac{\pi}{6}) \lt \displaystyle \frac{\sqrt{2}}{2}=\displaystyle \frac{1}{\sqrt{2}}$

$0 \leqq \theta \lt 2\pi$ のとき

$\displaystyle \frac{\pi}{6} \leqq \theta+\displaystyle \frac{\pi}{6} \lt \displaystyle \frac{13}{6}\pi$
下図のようになります。

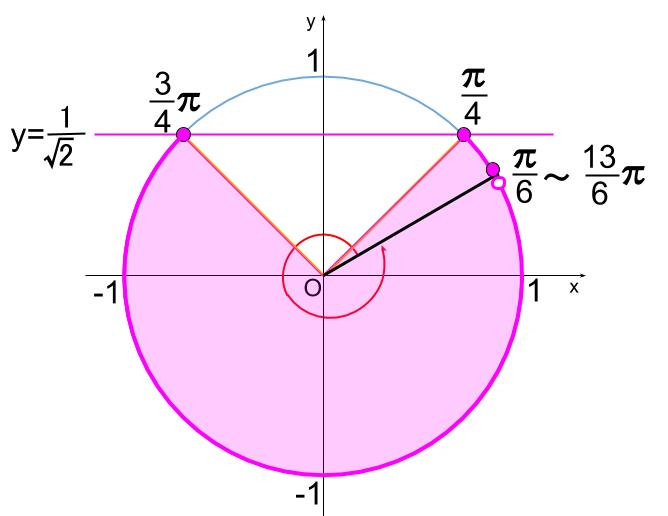
$\displaystyle \frac{\pi}{6} \leqq \theta+\displaystyle \frac{\pi}{6} \leqq \displaystyle \frac{\pi}{4}$ と $\displaystyle \frac{3}{4}\pi \leqq \theta+\displaystyle \frac{\pi}{6} \lt \displaystyle \frac{13}{6}\pi$

したがって、$0 \leqq \theta \leqq \displaystyle \frac{\pi}{12}$ と $\displaystyle \frac{7}{12}\pi \leqq \theta \lt 2\pi$