ポイント

最大値、最小値は、グラフをかいて解きましょう。

結局は、\(1\) 次関数か \(2\) 次関数の処理になります。

\(\sin \theta=t\) あるいは \(\cos \theta=t\) などと置き換えて
\(t\) の \(1\) 次関数（直線）として解きましょう。

あるいは、
\(\sin^2 \theta +\cos^2 \theta =1\)
を用いて、\(\sin \theta\) あるいは \(\cos \theta\) だけの \(2\) 次式にします。
その後は \(\sin \theta=t\) あるいは \(\cos \theta=t\) などと置き換えて、
\(t\) の \(2\) 次関数（放物線）の処理です。

いずれの場合も、\(t\) の取り得る値の範囲に注意しましょう。

例題１

\(0 \leqq \theta \lt 2\pi\) のとき、次の関数の最大値、最小値 を求めなさい。
また、そのときの \( \theta \) の値を求めなさい。

\(y=\displaystyle \frac{2}{3}\sin \theta +1\)

解説

\(\sin \theta\) を \(t\) とおくと \(-1 \leqq t \leqq 1\) ・・・①

このとき、\(y=\displaystyle \frac{2}{3}\sin \theta +1\) は、

\(y=\displaystyle \frac{2}{3}t +1\)

グラフは①の範囲で以下のようになります。

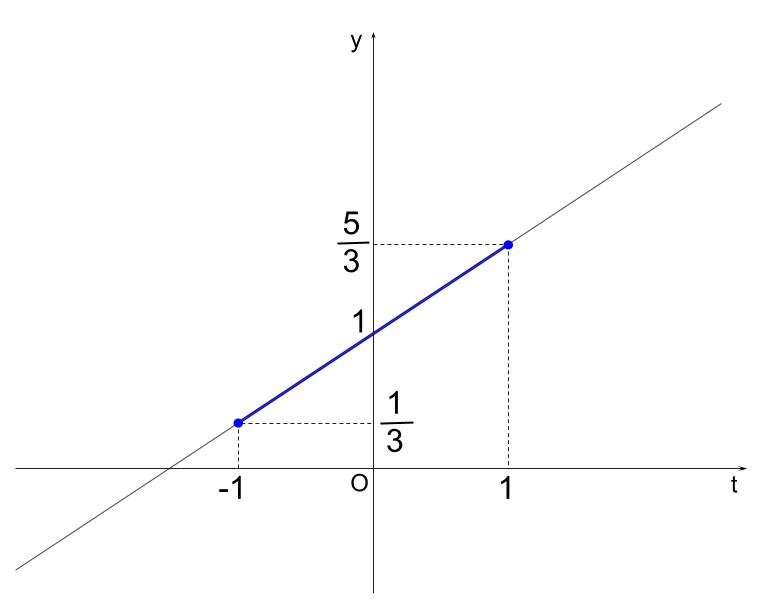
グラフより、

\(t=-1\) のとき、最小値 \(\displaystyle \frac{1}{3}\)、\(t=1\) のとき、最大値 \(\displaystyle \frac{5}{3}\) です。

つまり、

\(t=\sin \theta =-1\) のとき、 \(\theta =\displaystyle \frac{3}{2}\pi\) なので、\(\theta =\displaystyle \frac{3}{2}\pi\) で、最小値 \(\displaystyle \frac{1}{3}\)

\(t=\sin \theta=1\) のとき、 \(\theta =\displaystyle \frac{\pi}{2}\) なので、\(\theta =\displaystyle \frac{\pi}{2}\) で、最大値 \(\displaystyle \frac{5}{3}\)

例題２

\(0 \leqq \theta \lt 2\pi\) のとき、次の関数の最大値、最小値 を求めなさい。
また、そのときの \( \theta \) の値を求めなさい。

\(y=\sin^2 \theta – \cos \theta +1\)

解説

\(\sin^2 \theta +\cos^2 \theta =1\) を用いて、
\(y=\sin^2 \theta – \cos \theta +1\) を \(\cos \theta\) だけの式にします。

\(y=(1-\cos^2 \theta) – \cos \theta +1\)
\(y=-\cos^2 \theta – \cos \theta +2\)

\(\cos \theta =t\) とおくと \(-1 \leqq t \leqq 1\) ・・・①

このとき、\(y=-\cos^2 \theta – \cos \theta +2\) は、

\(y=-t^2-t+2\)

平方完成してグラフをかきます。
\(y=-(t+\displaystyle \frac{1}{2})^2+\displaystyle \frac{9}{4}\)

また、\(y=-t^2-t+2=-(t-1)(t+2)\) なので、 \(t\) 軸との交点もわかります。
①の範囲でグラフは以下のようになります。

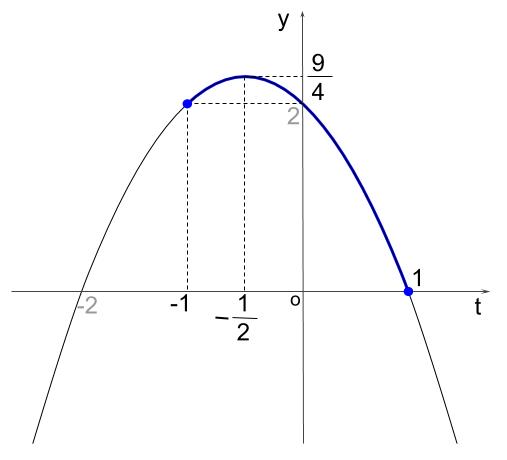
グラフより、

\(t=-\displaystyle \frac{1}{2}\) つまり、\(\cos \theta =-\displaystyle \frac{1}{2}\) で最大値 \(\displaystyle \frac{9}{4}\) をとり、

\(t=1\) つまり、\(\cos \theta =1\) で最小値 \(0\) をとります。

\(0 \leqq \theta \lt 2\pi\) で \(\theta\) について解くと、

\(\cos \theta =-\displaystyle \frac{1}{2}\) つまり、 \(\theta =\displaystyle \frac{2}{3}\pi, \displaystyle \frac{4}{3}\pi\) のとき、最大値 \(\displaystyle \frac{9}{4}\)

\(\cos \theta =1\) つまり、\(\theta =0\)　のとき、最小値 \(0\)