曲線の囲む面積

定積分によって、面積が求められることを学習しました。

次は、\(2\) つの曲線にはさまれた部分の面積です。

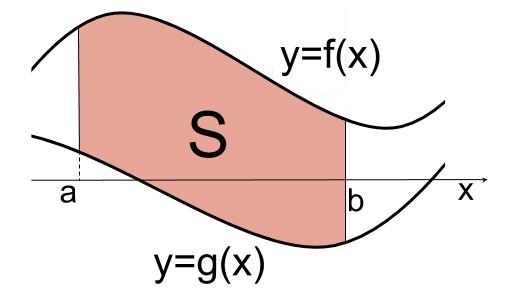
\(2\) 曲線で囲まれた部分の面積を求めるとき、 \(x\) 軸との位置関係は考える必要はありません。

また、\(f(x)\) や \(g(x)\) が直線であっても成り立ちます。

\(x\) 軸との間の面積

前回学習した、 曲線 \(y=f(x)\) と \(x\) 軸との間の面積も、上の説明にまとめられます。

\(x\) 軸とは \(y=0\) のことなので、
曲線 \(y=f(x)\) と \(y=0\) および、 \(2\) 直線 \(x=a,x=b\) とで囲まれた部分の面積 \(S\) は、

\(S=\displaystyle \int_a^b \{f(x)-0\} dx=\displaystyle \int_a^b f(x) dx\)

曲線 \(y=f(x)\) が \(x\) 軸より下にあるときの面積も同様で、

曲線 \(y=0\) と\(y=f(x)\) および、 \(2\) 直線 \(x=a,x=b\) とで囲まれた部分の面積 \(S\) は、

\(S=\displaystyle \int_a^b \{0-f(x)\} dx=\displaystyle \int_a^b -f(x) dx=-\displaystyle \int_a^b f(x) dx\)

例題１

次の曲線と直線とで囲まれた部分の面積を求めなさい。
\(y=x^2+1\)
\(y=-(x-1)^2\)
\(x=-1\)
\(x=2\)

解説

大雑把にグラフを図示して、上下関係を見ます。

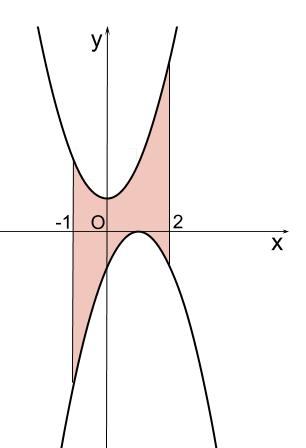
「上－下」を定積分します。

\(\displaystyle \int_{-1}^2 \{(x^2+1)-(-x^2+2x-1)\} dx \)

\(=\displaystyle \int_{-1}^2 (2x^2-2x+2) dx \)

\(=2\displaystyle \int_{-1}^2 (x^2-x+1) dx \)

\(= 2\left[ \displaystyle \frac{1}{3}x^3-\displaystyle \frac{1}{2}x^2+x \right]_{-1}^2\)

\(\begin{eqnarray}= & & \displaystyle \frac{2}{3}\{2^3-(-1)^3\} \\ &-& \hspace{ 4pt }\hspace{ 1pt }\{2^2-(-1)^2\} \\ &+& \hspace{ 6pt }2\{2\hspace{ 4pt }-(-1)\hspace{ 4pt }\} \end{eqnarray}\)

\(=9\)

おススメしませんが、\(F(2)-F(-1)\) を律儀に計算するならば、
\(=2\{\displaystyle \frac{1}{3}\cdot2^3-\displaystyle \frac{1}{2}\cdot2^2+2\}\)\(-2\{\displaystyle \frac{1}{3}\cdot(-1)^3-\displaystyle \frac{1}{2}\cdot(-1)^2+(-1)\} \)

\(=\displaystyle \frac{16}{3}-(-\displaystyle \frac{11}{3})\)

\(=9\)

例題２

次の曲線と直線とで囲まれた部分の面積を求めなさい。
\(y=x^2-1\)
\(y=-x^2+3x+4\)
\(x=-1\)
\(x=1\)

解説

どちらが上にあるのか、確かめます。
交点があるときは、交点を求めます。

\(x^2-1=-x^2+3x+4\) より
\(2x^2-3x-5=0\)
\((2x-5)(x+1)=0\)

\(x=-1,\displaystyle \frac{5}{2}\)

よって下図のようになります。

その後の面積計算↓

\(\displaystyle \int_{-1}^1 \{-x^2+3x+4-(x^2-1)\} dx \)

\(=\displaystyle \int_{-1}^1 (-2x^2+3x+5) dx \)

積分区間が \(-1\) から \(1\) までなので、
奇関数の積分は \(0\) です。

よって、計算が楽になりますね。

\(\displaystyle \int_{-1}^1 (-2x^2+3x+5) dx \)

\(=2\displaystyle \int_0^1 (-2x^2+5) dx \)

\(= 2\left[ -\displaystyle \frac{2}{3}x^3+5x \right]_0^1 \)

\(=2(-\displaystyle \frac{2}{3}\cdot1^3+5\cdot1)= \displaystyle \frac{26}{3} \)

例題３

次の曲線と直線とで囲まれた部分の面積を求めなさい。
\(y=\displaystyle \frac{1}{2}x^2-2\)
\(y=\displaystyle \frac{1}{2}x-1\)
\(x=-2\)
\(x=1\)

解説

どちらが上にあるのか、確かめます。
交点があるときは、交点を求めます。

\(\displaystyle \frac{1}{2}x^2-2=\displaystyle \frac{1}{2}x-1\)

\(\displaystyle \frac{1}{2}x^2-\displaystyle \frac{1}{2}x-1=0\)

\(x^2-x-2=0\)
\((x+1)(x-2)=0\)
\(x=-1,2\)

よって下図のようになります。

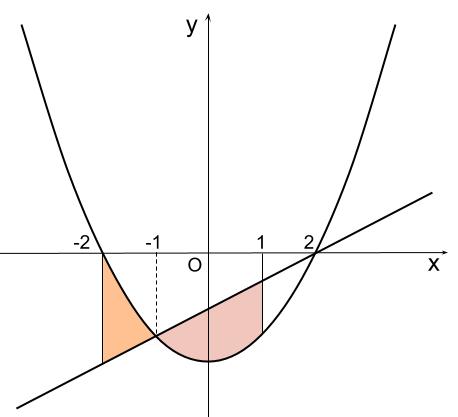
つまり、
\(-2 \lt x \lt -1\) では、 \(y=\displaystyle \frac{1}{2}x^2-2\)　が上

\(-1 \lt x \lt 1\) では、 \(y=\displaystyle \frac{1}{2}x-1\)　が上

よって、積分区間を分けて面積を求めます。

\(-2 \lt x \lt -1\)

\(\displaystyle \int_{-2}^{-1} \{\displaystyle \frac{1}{2}x^2-2-(\displaystyle \frac{1}{2}x-1)\} dx \)

\(=\displaystyle \int_{-2}^{-1} (\displaystyle \frac{1}{2}x^2-\displaystyle \frac{1}{2}x-1) dx \)

\(= \left[ \displaystyle \frac{1}{6}x^3-\displaystyle \frac{1}{4}x^2-x \right]_{-2}^{-1} \)

\(\begin{eqnarray}= & & \displaystyle \frac{1}{6}\{(-1)^3-(-2)^3\} \\ &-& \displaystyle \frac{1}{4}\hspace{ 0pt }\hspace{ 1pt }\{(-1)^2-(-2)^2\} \\ &-& \hspace{ 10pt }\{(-1)\hspace{ 4pt }-(-2)\hspace{ 4pt }\} \end{eqnarray}\)

\(=\displaystyle \frac{11}{12}\)

\(-1 \lt x \lt 1\)

\(\displaystyle \int_{-1}^1 \{\displaystyle \frac{1}{2}x-1-(\displaystyle \frac{1}{2}x^2-2)\} dx \)

\(=\displaystyle \int_{-1}^1 (-\displaystyle \frac{1}{2}x^2+\displaystyle \frac{1}{2}x+1) dx \)

\(=2\displaystyle \int_0^1 (-\displaystyle \frac{1}{2}x^2+1) dx \)

\(= 2\left[ -\displaystyle \frac{1}{6}x^3+x \right]_0^1 \)

\(=\displaystyle \frac{5}{3}\)

よって、求める面積は、

\(\displaystyle \frac{11}{12}+\displaystyle \frac{5}{3}=\displaystyle \frac{31}{12}\)