直線・曲線の囲む部分の面積 \(\displaystyle \frac{1}{6}\)公式の利用

公式

\(\displaystyle \int_\alpha^\beta (x-\alpha)(x-\beta) dx= -\displaystyle \frac{1}{6}(\beta-\alpha)^3 \)

を面積を求めるときに使用できるタイプを学習します。

どのようなときに使えるかというと、

\(y=f(x)\) と \(y=g(x)\) だけに囲まれた部分の面積を求めるときです。
より正確に補足すると、\(\{f(x)-g(x)\}\) が \(2\) 次式になるときです。

\(f(x)-g(x)=ax^2+bx+c=a(x-\alpha)(x-\beta)\) ならば、

\(y=f(x)\) と \(y=g(x)\) に囲まれた部分の面積は、

\(\displaystyle \int_\alpha^\beta \{f(x)-g(x)\} dx\)

\(=\displaystyle \int_\alpha^\beta a(x-\alpha)(x-\beta) dx\)

\(=a\displaystyle \int_\alpha^\beta (x-\alpha)(x-\beta) dx\)

\(=a×\{-\displaystyle \frac{1}{6}(\beta-\alpha)^3\} \)

例題１

次の曲線と直線とで囲まれた部分の面積を求めなさい。
\(y=-x^2+x+6\)
\(x\) 軸

解説

\(y=-x^2+x+6\)
\(=-(x+2)(x-3)\)

よって、下図のようになっています。

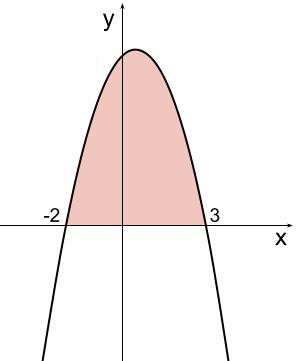
\(S=\displaystyle \int_{-2}^3 (-x^2+x+6) dx\)

\(=\displaystyle \int_{-2}^3 -(x^2-x-6) dx\)

\(=-\displaystyle \int_{-2}^3 (x+2)(x-3) dx\)

\(=-\displaystyle \int_{-2}^3 \{x-(-2)\}(x-3) dx\)

これは公式

\(\displaystyle \int_\alpha^\beta (x-\alpha)(x-\beta) dx= -\displaystyle \frac{1}{6}(\beta-\alpha)^3 \)

が使える形です。

\(-\displaystyle \int_{-2}^3 \{x-(-2)\}(x-3) dx\)

\(=(-1)×-\displaystyle \frac{1}{6}\{3-(-2)\}^3\)

\(=\displaystyle \frac{125}{6}\)

例題２

次の曲線と直線とで囲まれた部分の面積を求めなさい。
\(y=-2x^2+12x\)
\(y=2x+8\)

解説

放物線と直線の交点を求めます。

\(-2x^2+12x=2x+8\)
\(-2x^2+10x-8=0\)
\(x^2-5x+4=0\)
\((x-1)(x-4)=0\)
\(x=1,4\)
よって、下図のようになります。

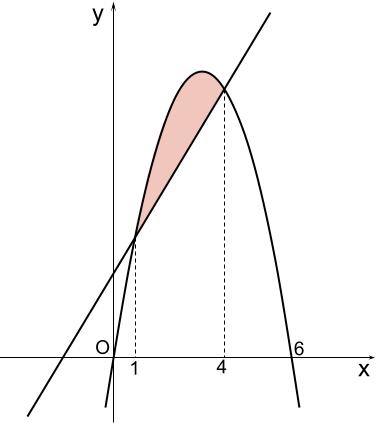
\(S=\displaystyle \int_1^4 \{-2x^2+12x)-(2x+8)\}dx\)

\(=\displaystyle \int_1^4 (-2x^2+10x-8) dx\)

\(=\displaystyle \int_1^4 -2(x-1)(x-4) dx\)

\(=-2\displaystyle \int_1^4 (x-1)(x-4) dx\)
※交点を求めた時点で、この形に式変形できることがわかります。

これは公式

\(\displaystyle \int_\alpha^\beta (x-\alpha)(x-\beta) dx= -\displaystyle \frac{1}{6}(\beta-\alpha)^3 \)

が使える形です。

\(-2\displaystyle \int_1^4 (x-1)(x-4) dx\)

\(=(-2)×\{-\displaystyle \frac{1}{6}(4-1)^3\}\)

\(=9\)

例題３

次の \(2\) つの曲線に囲まれた部分の面積を求めなさい。
\(y=x^2+1\)
\(y=-x^2+2x+1\)

解説

\(2\) つの放物線の交点を求めます。

\(x^2+1=-x^2+2x+1\)
\(2x^2-2x=0\)
\(2x(x-1)=0\)
\(x=0,1\)
よって、下図のようになります。

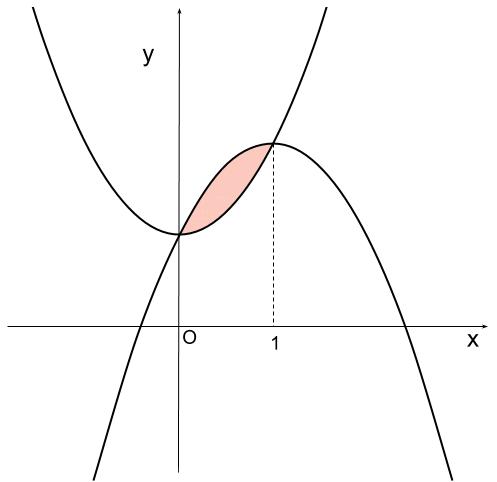
\(S=\displaystyle \int_0^1 \{(-x^2+2x+1)-(x^2+1)\}dx\)

\(=\displaystyle \int_0^1 (-2x^2+2x) dx\)

\(=\displaystyle \int_0^1 -2x(x-1) dx\)

\(=-2\displaystyle \int_0^1 (x-0)(x-1) dx\)
※交点を求めた時点で、この形に式変形できることがわかります。
これは公式

\(\displaystyle \int_\alpha^\beta (x-\alpha)(x-\beta) dx= -\displaystyle \frac{1}{6}(\beta-\alpha)^3 \)

が使える形です。

\(-2\displaystyle \int_0^1 (x-0)(x-1) dx\)

\(=(-2)×\{-\displaystyle \frac{1}{6}(1-0)^3\}\)

\(=\displaystyle \frac{1}{3}\)